Geoscience Reference
In-Depth Information
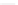
∂χ
THL
∂z
Here the term in parentheses on the right-hand sides
of each of equations (1.25) and (1.27) is effectively the
stream function
χ
GM
for the eddy-induced azimuthal
mean flow
(u
∗
,
w
∗
)
in the meridional
(r
,
z)
plane.
Gent and
McWilliams
[1990] proposed that the buoyancy flux in
this definition of
χ
∗
be parameterized as a down-gradient
diffusion of zonallyaveraged buoyancy
χ
GM
=
u
ρ
=
−
,
(1.33)
w
THL
=
∂χ
THL
,
(1.34)
∂y
where
K
q
(y
,
z)
is again a suitably defined eddy diffu-
sion coefficient, this time for potential vorticity
q
, and is
assumed here to be variable in space.
A complete understanding of all of these issues there-
fore remains elusive, and there remains a continuing prob-
lem of how to verify any scheme of parameterization
with the desired degree of rigor. In this respect, labora-
tory experiments such as the rotating, thermally driven
annulus ought to have something important to contribute.
Experimental techniques have been available for some
time to measure both the total heat transport across the
annular cavity (e.g., via calorimetric methods to deter-
mine the total heat transport across a given sidewall
boundary)
and
the interior eddy variances and fluxes of
heat, momentum, and vorticity associated with baroclinic
waves. The quantitative interpretation of these measure-
ments, however, requires a clear understanding of the
various mechanisms at work within rotating annulus cir-
culations to transport heat energy across the annular
channel. These include direct thermal conduction and
direct overturning circulations (mainly in boundary lay-
ers) as well as macroturbulent transports by baroclinic
eddies themselves. In subsequent sections, therefore, we
examine and review the main boundary layer and eddy
processes that contribute to heat transport in the annu-
lus, culminating in some preliminary attempts to apply
an analogue of ocean baroclinic eddy parameterization
schemes within an axisymmetric numerical annulus model
in which baroclinic instability is artificially suppressed.
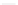
=
K
,
∂ρ/∂y
∂ρ/∂z
−
(1.29)
∂ρ/∂z
where
is a suitably defined eddy diffusion coefficient that
needs to be completed with a suitable closure model. The
latter is commonly assumed to take the general form
K
K
=
αL
eddy
U
eddy
,
(1.30)
where
L
eddy
and
U
eddy
are characteristic scales for eddy
length and velocity scales and
α
is a dimensionless
constant, found empirically to require a value
O
(10
−
2
)
[e.g.,
Visbeck et al.
, 1997;
Marshall and Adcroft
, 2010].
There remains significant uncertainty, however, as
to the physical basis for choosing
L
eddy
and
U
eddy
.
L
eddy
represents a prescribed “mixing length”, sug-
gestions for which have included either the so-called-
Rhines scale
L
Rhines
=
(U
rms
/β)
1
/
2
[
Larichev and Held
,
1995;
Treguier et al.
, 1997], the width of the baro-
clinic zone [
Green
, 1970;
Visbeck et al.
, 1997], or
the Rossby deformation radius [
Stone
, 1972].
U
eddy
has been taken variously as either a “typical” ther-
mal wind scale related to the zonal mean horizon-
tal thermal gradient [
Green
, 1970] or setting
U
eddy
∼
L
eddy
/τ
eddy
,where
τ
eddy
is a “typical” eddy overturning
time scale that might be derived, for example, from lin-
ear baroclinic instability theory [
Stone
, 1972;
Haine and
Marshall
, 1998] or weakly nonlinear theory [
Pfeffer and
Barcilon
, 1978;
Read
, 2003]. In addition, problems may
arise if a parameterization scheme fails to respect key
conservation principles, especially energy and potential
vorticity [e.g.,
Marshall and Adcroft
, 2010]. The parame-
terization of the eddy-driven “bolus” velocity from zonal
mean fields is another controversial issue since it is not
always clear that the horizontal eddy buoyancy flux nec-
essarily acts diffusively down gradient with respect to the
zonal mean buoyancy field [e.g.,
Treguier et al.
, 1997;
Marshall and Adcroft
, 2010].
Treguier et al.
[1997] and
Killworth
[1997] suggested an alternative approach based
on assuming that potential vorticity is more generally dif-
fused down gradient than pure buoyancy such that the
eddy-induced velocity
(u
∗
,
w
∗
)
is defined as
1.4.2. Regimes of Axisymmetric Flow: Heat and
Momentum Transport
Although the description of the axisymmetric flow in
the introduction to this section gave a plausible explana-
tion for the observed axisymmetric and wave regimes in
the annulus, it is a highly simplified discussion that glosses
over more subtle aspects of the problem. In this section,
we take a more quantitative view of the axisymmetric flow
in the annulus to put the above discussion onto a stronger
theoretical footing and as an illustration of the use of scale
analysis and boundary layer theory.
Early analyses [
McIntyre
, 1968;
Sugata and Yoden
,
1992] followed the scaling approach developed by
Gill
[1966], which
Hignett et al.
[1981] and
Hignett
[1982] fur-
ther extended for an incompressible Boussinesq fluid in
a rotating annulus of vanishingly small relative curvature
(2
u
ρ
∂ρ/∂z
∂
∂z
u
THL
=
−
(1.31)
u
q
f
K
(y
,
z)∂q/∂r
f
−
(1.32)
[
b
−
a
]
/
[
b
+
a
]
1, so one may use Cartesian geometry)