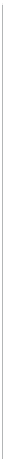Geoscience Reference
In-Depth Information
the inner and outer cylinder and the depth of the annulus,
respectively. Figure 1.3 shows a schematic form of this
diagram with the locations of the main regimes indicated.
From a consideration of the conditions under which
waves occur in the annulus (especially the location in the
parameter space of the upper-symmetric transition) and
a comparison with the results of linear instability the-
ory, it is clear that the waves in the annulus are fully
developed manifestations of baroclinic instability (often
referred to as “sloping convection” from the geometry
of typical fluid trajectories; for example, see
Hide and
Mason
[1975]). Since these flows occur in the interior
of the annulus (i.e., outside ageostrophic boundary lay-
ers) under conditions appropriate to quasi-geostrophic
scaling, a dynamical similarity to the large-scale midlat-
itude cyclones in Earth's atmosphere is readily apparent,
though with rather different boundary conditions. A more
detailed discussion of the properties of these flows is
given below and by
Hide and Mason
[1975] and
Ghil and
Childress
[1987]. Associated with this conclusion is the
implication that the waves develop in order to assist in
the transfer of heat both upward (enhancing the static
stability) and horizontally down the impressed thermal
gradient (i.e., tending to reduce the impressed horizontal
gradient). The action of heat transport by the waves and
axisymmetric flows will be considered in the next section.
1
Δ
ρ
ρ
= 10
-4
10
-3
10
-2
m
= 1
2
3
4
10
100
31.6
316
1000
3160s
5
6
7
8
9
10
11
12
13
14
15
10
-1
10
-2
10
-3
10
-8
10
-7
10
-6
10
-5
10
-4
10
4
10
5
10
6
Ta
10
7
10
8
Figure 1.4.
Regime diagram based on the extension of Eady's
baroclinic instability theory to include Ekman layers and flat,
horizontal boundaries. The wave number of maximum insta-
bility is indicated by integer numbers and the transition curves
and contours of e-folding time are given on a Burger number
(Bu
plot. (Adapted
from
Mason
[1975] by permission of the Royal Society).
∼
;see
Hide and Mason
[1975]) against
T
1.3.2. Axisymmetric/Wave Transition and Linear
Instability Theory
The previous section indicated the conditions under
which baroclinic waves occur in the annulus and their
role as a means of transferring heat upward and against
the horizontal temperature gradient. The Eady model of
baroclinic instability has been commonly invoked as an
idealized, linearized conceptual model to account for the
onset of waves from axisymmetric flow [
Hide
, 1970;
Hide
and Mason
, 1975,
Ghil and Childress
, 1987]. Although the
Eady model is highly idealized, it does seem to predict the
location of the onset of large-amplitude waves remarkably
close to the conditions actually observed, at least at high
Taylor number (note that the Eady problem in its “classi-
cal form” is inviscid). Apparent agreement can be made
even closer if the Eady problem is modified to include
Ekman boundary layers by replacing the
w
= 0 boundary
condition with the Ekman compatibility condition
Taylor number (see Figure 1.4), supporting the hypothesis
[
Hide and Mason
, 1975] that the “lower symmetric transi-
tion” is frictionally dominated.
The structure of the most rapidly growing instability
has certain characteristic features in terms of, for example,
phase tilts with height. In the thermal annulus, steady
baroclinic waves are also seen to exhibit many of these
features, as determined from experiment and numerical
simulation. The extent to which Eady theory actually pro-
vides a complete theoretical description of the instability
problem in annulus experiments, however, is a somewhat
more complicated question than it at first appears. The
dominant instability in the Eady model relies on the exis-
tence of horizontal temperature gradients on horizontal
boundaries for the required change of sign in the l
a
teral
gradient of quasi-geostrophic potential vorticity,
∂q/∂y
,
for instability [e.g.,
Charney and Ste
rn
, 1962]. Elsewhere,
the flow is constructed such that
∂q/∂y
=0.Inprac-
tice, however, strong horizontal mass transports in the
Ekman layers result in almost no horizo
nt
al tempera-
ture gradients at the boundaries; in reality
∂q/∂y
changes
sign smoothly in the interior (e.g., see Figure 1.17c later).
Thus, instability of an internal baroclinic jet is arguably
a more appropriate starting point, preferably including a
1
/
2
√
2Ro
∇
w
=
E
2
ψ
,
z
= 0,1,
(1.4)
where
ψ
is the stream function for the horizontal flow.
This naturally brings in the Taylor number familiar
to experimentalists (via Ekman number
) and leads
to a plausibly realistic envelope of instability at low
E