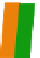Upscaling Flow Properties - Reservoir Model Design - page 126

Gravity dominated

Reality ?

Viscous dominated Capillary dominated

Fig. 4.13 The fluid forces triangle with sketches to illustrate how a water-flood would behave for a layered rock
( yellow ¼ high permeability layers)

gradient term, while the gravity/capillary ratio is
the buoyancy term against the capillary pressure
gradient. z represent the physical length

scales - essentially the size of the model in the x
and z directions. There are several different
forms of derivation of these ratios depending on
the physical assumptions and the mathematical
approach, but the form given above should allow
the practitioner to gain an appreciation of the
factors involved. It is important that a consistent
set of units are used to ensure the ratios remain
dimensionless.
For example, a calculation to determine when
capillary/heterogeneity interactions are impor-
tant can be made by studying the ratio of capil-
lary to viscous forces. Figure 4.14 shows a
reference well pair assuming 1 km well spacing
and a 150 psi pressure drawdown at the produc-
ing well. We are interested in the balance of
forces and a rock unit within the reservoir,
represented by alternating permeability layers
with a spacing of

ʔ x and ʔ

150psi

x
1 km

D

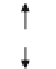
Fig. 4.14 Sketch of pressure drawdown between an
injection and production well pair for water-flooding an
oil reservoir

ratio for different layer contrasts and heterogene-
ity length-scales (Ringrose et al. 1996 ).
If the layering in a reservoir occurs at the

> 10 m scale then viscous forces tend to dominate

(or the Viscous/Capillary ratio must be very low
for capillary forces to be significant at this scale).
However, if the layers are in the mm-to-cm range
then capillary forces are much more likely to be
important (or the Viscous/Capillary ratio must be

x. Figure 4.15 shows the
result of the analysis of the viscous/capillary

ʔ