Geoscience Reference
In-Depth Information
seismic wave energy at a planar interface, and
then subsequently many others (notably Shuey
1985
) developed approaches for determining
rock properties from seismic waves. Because
there is a relationship between the reflection
coefficient, R, and the angle of incidence,
different volumes with the reservoir - well data
needs to be upscaled and seismic data needs to be
downscaled (depending on the grid resolution
and seismic resolution of the case in hand). This
is where the Bayesian method comes into play.
Buland et al. (
2003
) developed a particularly
elegant and effective method for estimating rock
properties from AVO data, employing Bayesian
inference and the Fourier transform. This
approach allows the reservoir modeller to recon-
cile different scales of data (seismic versus well
data, using the Fourier transform) within a robust
Bayesian statistical framework: what is the best
seismic inversion given the well data - a P(A|
,
analysis of seismic amplitude variations with
offset (AVO) or angle (AVA) allows rock
properties of specific rock layers to be estimated.
The simplest form of the AVO equations,
known as the Shuey approximation is:
R
ʸ
G
sin
2
ðÞ
¼
R0
ðÞþ
ʸ
ð
3
:
28
Þ
Where R(0) and R(
ʸ
) are the reflection
)
problem. Nair et al. (
2012
) have illustrated this
workflow for reservoir characterization, combin-
ing elastic properties (from seismic) with facies
probability parameters (from wells) to condition
probabilistic property models.
Having first extracted elastic properties (V
P
,
V
S
and
Β
coefficients for normal
incidence and offset
angle
ʸ
and G is a function of V
P
and V
S
, given
by:
2
V
S
V
P
1
2
ʔ
V
P
V
P
ʔˁ
ˁ
þ
2
ʔ
V
S
V
S
G
¼
ð
3
:
29
Þ
Subsequently, using empirical correlations, it
is then possible to estimate porosity from V
P
,V
S
and
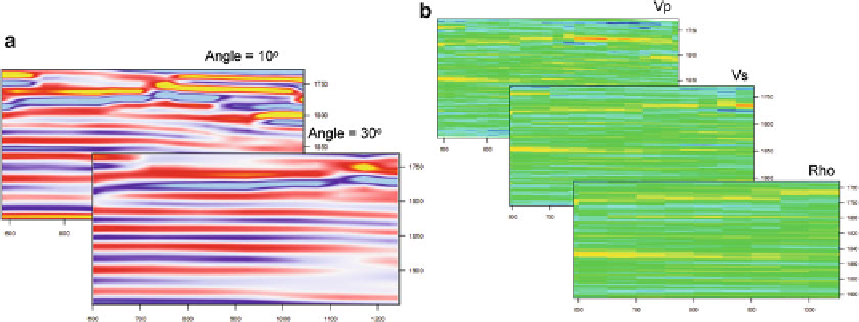
from the seismic AVA data (Fig.
3.25
),
the challenge is then to relate elastic properties
to flow properties.
Since flow properties are essentially estimated
from well data (cores and logs), we need to
merge (or correlate) the seismic elastic properties
with elastic and flow properties at the wells.
This is a complicated process. We need a veloc-
ity model to convert seismic data from time to
depth and we need a way handling the scale
ˁ
. Assuming that information on rock
properties can be gained from seismic data, the
next challenge is to find a way of integrating
seismic information with well data and the
underlying geological concepts. The real chal-
lenge here is that well data and seismic data
rarely tell the same story - they need to be
reconciled. Both seismic data and well data
have associated uncertainties. They also sample
ˁ
Fig. 3.25
(
a
) Angle stacks and (
b
) corresponding
inverted elastic parameters from seismic inversion
case study (From Nair et al.
2012
)(Redrawnfrom
Nair et al.
2012
,
#
EAGE reproduced with kind
permission
of EAGE Publications B.V., The
Netherlands)