Reference Ellipsoid and the Geodetic Coordinate System - Geodesy: Introduction to Geodetic Datum and Geodetic Systems - page 208

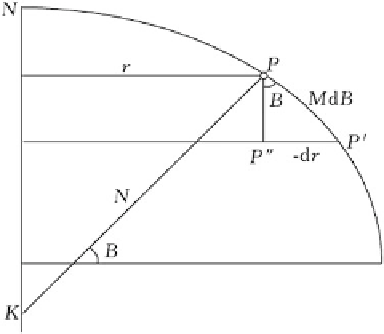
Fig. 5.27 Computation of
dr using meridian arc
element

r sin A ﾼ C : ð 5 : 53 Þ

This is known as Clairaut's equation for the geodesic (e.g., as described in
Thomas and Featherstone 2005), which shows that the product of the radius of
the parallel and the sine of the geodesic azimuth at any point along the geodesic is a
constant.

5.4.6 Solution of Ellipsoidal Triangles

After establishing the corresponding relationships between the Earth's surface and
the surface of the ellipsoid, the terrestrial control network will become the control
network formed by geodesics on the ellipsoid. The unobserved sides and angles of
the control network must be computed using ellipsoidal triangles. Since the curva-
tures at each point on the ellipsoid are different, it is rather complicated to solve
triangles on the ellipsoid. However, the flattening of the Earth ellipsoid is very
small, and the ellipsoidal triangle formed by the three sides in the geodetic control
network is usually quite small; therefore, it may be possible to solve the ellipsoidal
triangle as a spherical triangle. Research has shown that when the sides of the
triangle are less than 200 km, it is completely viable to approximate the ellipsoidal
triangle as a spherical triangle, and the spherical radius is the mean radius of
curvature at the mean latitude of the three vertices of the ellipsoidal triangle.
(The sides of the spherical triangle are equal in length to the corresponding sides
of the ellipsoidal triangle, while the difference in the corresponding angles of the
two triangles is less than 0.001 00 .)
The sine formula below is applied to solve the spherical triangle: