Geoscience Reference
In-Depth Information
Figure 3.5
Isobars and isopycnals (dashed) in
the vertical plane n-z where n is the direction
of largest horizontal pressure gradient. In (a)
density is constant or a function of z only so
isobars, including that at the sea surface, are
parallel to each other and to the isopycnals.
This is the barotropic case in which flow is
uniform in depth and directed into the paper
(Northern Hemisphere).
z
(a)
surface
z
=
η
p
1
r
1
p
2
r
2
p
3
r
3
p
4
r
4
p
5
q
n
z
In (b) density is a function of horizontal
position as well as depth. The isobars are
inclined to the isopycnals and to each other
in this baroclinic case.
(b)
d
p
=
0
p
1
q
p
2
r
1
p
3
r
2
p
4
r
3
p
5
r
4
n
the surface and the bulk water column density, i.e. set r
s
¼
r
0
, the geostrophic
balance in
Equation (3.18)
then gives the current speed as:
0
@
1
p
g
f
@
C
g
¼
n
¼
n
:
ð
3
:
23
Þ
@
@
f
We now see that C
g
depends only on the surface slope and is the same at all depths.
This situation is shown in
Fig. 3.5a
: when density is a function only of z, surfaces of
equal pressure (isobars) are parallel to each other and parallel to surfaces of equal
density (isopycnals). We refer to the flow as being barotropic.
(ii) The density
r
varies in x, y and z, i.e.
r
¼
r
(x,y,z)
In this case, isobars may be inclined relative to each other and to the isopycnals, a
situation of so-called baroclinic flow. Here it is most convenient to determine the
pressure gradient by reference to the slope of isobars. In the vertical z-n plane shown
in
Fig. 3.5b
, the slope of an isobar can be found from the conditions that the pressure
is invariant on an isobar and obeys the hydrostatic condition. So as we move along a
sloping isobar we can say that the pressure change will be:
¼
@
p
þ
@
p
p
n
n
z
z
¼
0
@
@
p
¼
ð
3
:
24
Þ
¼
@
=@
g
@
dz
dn
p
n
1
p
so that
tan
z
¼
@
p
=@
@
n










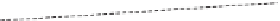

































Search WWH ::

Custom Search