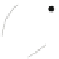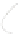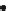Information Technology Reference
In-Depth Information
(a) weak embedding
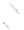
(b) strong embedding
(c) full embedding
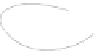
Fig. 1.
Examples of simultaneous embeddings of two partitions
universe
U
, i.e., each element
u ∈ U
is contained in one block of
P
0
and in one block
of
P
1
. In the following we often omit to mention
U
explicitly.
Let
S
be a collection of subsets of
U
.An
embedding
ʓ
of
S
maps every element
2
and every set
S
u
∈
U
to a distinct point
ʓ
(
u
)
∈
R
∈S
to a simple, bounded, and
2
closed region
ʓ
(
S
)
S
. Moreover,
we require that each contiguous intersection between the boundaries of two regions is
in fact a
crossing point
p
ↂ
R
such that
ʓ
(
u
)
∈
ʓ
(
S
) if and only if
u
∈
2
, i.e., the local cyclic order of the boundaries alternates
around
p
.A
simultaneousembedding
ʓ
of a pair of partitions
∈
R
{P
0
,
P
1
}
is an embedding
of the union
P
0
∪P
1
of the two partitions. We define
R
B
=
ʓ
(
B
) as the
block region
of
ablock
B
and denote its boundary by
∂R
B
.Figure 1 shows examples of simultaneous
embeddings in the three different embedding classes to be defined in Section 2.
Asimultaneous embedding
ʓ
induces a subdivision of the plane and we can derive a
plane multigraph
G
ʓ
by introducing a node for each intersection of two boundaries and
an edge for each section of a boundary that lies between two intersections. Furthermore,
aboundary without intersections is replaced by a node with a self loop nested inside its
surrounding face. We call
G
ʓ
the
contour graph
of
ʓ
and its dual graph
G
ʓ
the
dual
graph
of
ʓ
. The faces of
G
ʓ
belong to zero, one, or two block regions. We call a face
that belongstonoblockregion a
backgroundface
, a face that belongstoasingle block
region a
linking face
, and a face that belongs to two block regions an
intersection face
.
Only intersection faces contain points corresponding to elements in the universe, and
no two faces of the same type are adjacent in the contour graph.
Alternatively, the union of the two partitions
P
0
∪P
1
can also be seen as a hyper-
graph
H
=(
U,P
0
∪P
1
), where every element
u ∈ U
is a vertex and every block
defines a hyperedge, i.e., a non-empty subset of
U
. The hypergraph
H
is
2-regular
since every vertex is contained in exactly two hyperedges. We denote
H
=
H
(
P
0
,P
1
)
as the
corresponding hypergraph
of the pair of partitions
.
Hypergraph supports
[15] play an important role in hypergraph embeddingsand
their planarity. A support of a hypergraph
H
=(
V,
{P
0
,
P
1
}
) is a graph
G
p
=(
V,E
) on
the vertices of
H
,such that the
induced subgraph
G
p
[
S
] of every hyperedge
S
S
is
connected. We extend the concept of supports to pairs of partitions, i.e., we say that a
graph
G
p
=(
V,E
) is a support for
∈S
P
1
).
We call a support
path based
,iftheinduced subgraphs of all hyperedges are paths,
1
and
tree based
, if all hyperedge-induced subgraphs are trees, i.e., they do not contain
{P
0
,
P
1
}
,ifitisasupport of
H
(
P
0
,
1
Brandes et al. [4] used a slightly different definition and called a support
path based
if the
induced subgraph of each hyperedge has a Hamiltonian path.