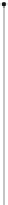Information Technology Reference
In-Depth Information
8
6
8
w
4
u
6
u
8
8
u
4
u
5
u
7
K
4
gadget
7
5
7
7
w
3
u
4
u
6
6
4
6
6
u
3
u
3
u
5
kite gadget
5
3
5
5
w
2
u
2
u
4
4
2
4
4
u
2
u
1
u
3
C
4
gadget
3
1
3
3
w
1
v
u
2
2
0
2
2
u
1
w
1
w
2
u
1
K
3
gadget
1
-1
1
1
v
v
0
-2
0
0
Fig. 5.
Illustration of the
y
-levelings described in the proof of Lemma 7. (a) A radius-2 star. (b)
Afull 1-connected extended degree-3 spider. (c) A 2-connected extended degree-3 spider (with
an edge replaced by a kite gadget). (d) A generalized caterpillar.
EAQP
. Since the tree
T
in Fig.6(a),
which is not in
AEP
[11], is in
EAQP
(see Fig.6(b)),wehave
AEP
From the discussion above we have
AEP
ↆ
=
EAQP
.
The proof of the next lemma is analogous to the one of Lemma 3.
Lemma 8.
Let
G
∈
EAQP
.Then
G
∈
AEQP
.
It is natural to ask whether
AEQP
and
EAQP
coincide or not. Also, it is natural to
study which families of graphs belong to
AEQP
and to
EAQP
. Theorem 5 answers
the first question and gives a result about the second research direction. Theorem 6
summarizes the relationships between
EAP
,
AEP
,
EAQP
,and
AEQP
.
Theorem 5.
All trees are AEQPgraphs andthere exist trees that are not EAQPgraphs.
Sketch of Proof:
The fact that every tree is an EAQPgraph follows easily from the result
in [8]. A tree that is not in
EAQP
is shown in Fig.6(c).
Theorem 6.
EAP
ↂ
AEP
ↂ
EAQP
ↂ
AEQP
.
In the next theorem we prove that
maximalouterpillars
are EAQPgraphs. An outer-
planar graph is called an
outerpillar
if its weak dual is a a
caterpillar
.Anouterpillar is
u
7
u
6
u
0
v
u
5
u
1
u
2
u
3
u
4
u
1
u
5
u
3
u
3
u
2
u
2
u
6
u
7
u
4
u
1
u
0
Fig. 6.
(a) A tree
T
that is an EAQPgraph but is not an AEPgraph. (b) A universal quasi planar
y
-leveling of
T
. (c) A tree that is not an EAQPgraph.