Information Technology Reference
In-Depth Information
kernel of
f
ʵ
last edge of
C
i
in
G
2
f
p
u
position of
G
[
C
i
]
v
2
last edge of
C
i
in
G
1
C
i
f
0
e
0
v
e
k
v
1
(a)
(b)
(c)
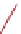
Fig. 2.
Illustration of the placement of the
G
[
C
i
] inside the face
f
for a (0
,
3)-drawing
Theorem 4.
Let
(
G
1
,G
2
)
be twoplanar graphs witha
S
EFE
embedding.Assumefur-
ther that
G
=
G
1
∩
G
2
is an induced subgraph of
G
1
and
G
2
, respectively.Ifeach
connected componentof
G
is biconnected, there exists a
(0
,
3)
-drawing of
(
G
1
,G
2
)
.
Sketch of Proof.
Withoutlossofgenerality, we can assume that
G
1
and
G
2
are internally
triangulated and that the outer face of
G
does not contain any exclusive edges. Let
C
be
a connected component of
G
and denote by
G
[
C
] the subgraph of
G
consisting of all
vertices and edges that either belong to
C
or are embedded inside some inner face of
C
.
The graphs
G
1
[
C
] and
G
2
[
C
] are defined analogously. Note that if
C
is a connected
component of
G
with
C
ↆ
G
[
C
],then
G
[
C
]
ↆ
G
[
C
]. Hence, the relation
C
≺
C
if and only if
G
[
C
]
G
[
C
] defines a partial ordering of the components of
G
whose
transitive reduction is a tree. We prove the following claim by induction on the depth of
this tree; it implies the statement of the theorem.
ↆ
Claim.
Let
C
be a connected component of
G
with depth
d
.Theinduced S
EFE
of
G
1
[
C
]
and
G
2
[
C
] admits a (0
,
3)-drawing such that the outer face of
G
[
C
] is star-shaped.
The base case, where
G
[
C
]=
C
is biconnected, follows from Theorem 1(i). For the
induction step, assume that
C
is a component such that
G
[
C
] has depth
d
.Thegraph
C
is biconnected, and we take a star-shaped drawing with positive kernel area in all faces.
Clearly, the outer face is star-shaped. We show that we can embed the remaining parts
of
G
1
[
C
] and
G
2
[
C
] inside the inner faces of
C
using the given embedding and such
that the result is a (0
,
3)-drawing. The faces of
C
can be treated independently. In the
following we fix an arbitrary internal face
f
and denote by
C
1
,...,C
c
the connected
components of
G
that are distinct from
C
and incident to
f
. Note that
G
[
C
i
] has depth
at most
d
1 and hence, by induction, we know that corresponding (0
,
3)-drawings
of
G
1
[
C
i
] and
G
2
[
C
i
] exist for
i
=1
,...,c
. We show how to arrange them in the
interior of
f
and how to draw the exclusive edges embedded inside
f
to obtain a (0
,
3)-
drawing of
G
1
[
C
] and
G
2
[
C
].Weassume that the only exclusive edges of
G
1
and
G
2
are the ones embedded inside
f
. This is not a restriction since there is no interaction
between exclusive edges in distinct faces of
G
. We can thus treat all faces independently.
Since
G
1
and
G
2
are triangulated, it follows that the subgraph induced by the ex-
clusive vertices of
G
i
that are embedded inside
f
is connected, and we contract it into
asingle vertex
v
i
for
i
=1
,
2, preserving the edgeordering of the given embedding.
−