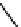Information Technology Reference
In-Depth Information
v
v
=
v
1
v
n
T
T
v
4
v
i
w
1
w
k
w
i
w
1
v
1
v
k
w
i
C
w
v
3
v
1
v
2
v
k
+1
w
k
Fig. 7.
Astrongly mono-
tone drawing of a bicon-
nected outerplanar graph
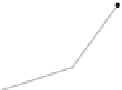
Fig. 8.
Aplanargraph with-
outanystrongly monotone
drawing
Fig. 6.
Subdivision of a vertex
v
with
k
outgoing edges
We close with a negative result. Note that the graphs in the family that we construct
are neither outerplanar nor biconnected.
Theorem 5.
There is an infinite family of connected planar graphsthatdonot have a
stronglymonotonedrawing in any combinatorialembedding.
Proof.
Let
C
be the graph that arises by attaching to each vertex of
K
4
a “leaf”; see
Fig.8.Let
v
1
,...,v
4
be the vertices of
K
4
.For
K
4
to be crossing-free, one of its ver-
tices, say
v
1
, lies in the interior. Let
w
be the leaf incident to
v
1
. Because of planarity,
w
has to be placed inside a triangular face incident to
v
1
. W.l.o.g., assume that
w
is placed
in the face (
v
1
,v
2
,v
3
). If the drawing is strongly monotone, then
(
−−
wv
2
,
−−
wv
1
)
<ˀ/
2
∠
(
−−
wv
3
,
−−
wv
2
)
>ˀ
. However, this means that
w
does not lie inside the triangle (
v
1
,v
2
,v
3
), which is a contradiction to the assumption.
Thus,
C
does not have a strongly monotone drawing in any combinatorial embedding.
We create an infinite family from
C
by adding more leaves to the vertices of
K
4
.
(
−−
wv
1
,
−−
wv
3
)
<ˀ/
2 and thus
and
∠
∠
5
Conclusion and Open Problems
We have shown that any tree has a monotone drawingsonagrid with area
O
(
n
3
) and a
strongly monotone drawing,but can we combine the two features, that is, does any tree
have a strongly monotone drawing on a grid of polynomial size?
Angelini et al. [2, Fig. 18(b)] have constructed a drawing of a triangulation that is
not strongly monotone. But is there a triconnected (or biconnected) planar graph that
does not have any strongly monotone drawing? If yes, can this be tested efficiently?
If we could show that ourdrawingsforgeneral trees are not just strongly monotone
but also convex (as in the proper binary case), then all Halin graphs would automatically
have convex and strictly monotone drawings, too.
References
1. Alamdari, S., Chan, T.M., Grant, E., Lubiw, A., Pathak, V.: Self-approachinggraphs. In:
Didimo, W., Patrignani, M. (eds.) GD 2012. LNCS, vol. 7704, pp. 260-271. Springer, Hei-
delberg (2013)
2. Angelini, P., Colasante, E., Battista, G.D., Frati, F., Patrignani, M.: Monotone drawingsof
graphs. J. Graph Algorithms Appl. 16(1), 5-35 (2012)