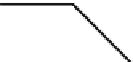Information Technology Reference
In-Depth Information
Second, we define three cones
C
1
,
C
2
,and
C
3
(see Fig.3).
Each cone has its apex at the origin and spans an angle of
ˀ/
4.
The angular ranges are
C
1
=[0
,ˀ/
4],
C
2
=[3
ˀ/
4
,ˀ
],and
C
3
=[3
ˀ/
2
,
7
ˀ/
4];angles are measured from the
x
-axis point-
ing in positive direction. Note that
C
2
is separated from the two
other cones by an angle of
ˀ/
2. As mentioned in Section 2 the
set
V
n
contains
n
primitive vectors in the [0
,d
]
ˀ/
2
C
2
C
1
ˀ/
2
ˀ/
4
C
3
[0
,d
] grid.
When reflected on the
x
=
y
line these vectors lie in
C
1
.Re-
flecting the vectors in
C
1
further we generate
n
vectors in
C
2
and
n
vectors in
C
3
. In every cone we “need” at most
n
×
Fig. 3.
The cones that
contain the slopes used
in the algorithm
3
edges, hence we can remove the vectors on the boundary of each cone. After removing
the temporary edges, the number of vectors will drop from 3
n
to
n
−
1.
Now, we observe the following. Every two consecutive edges incident to the root lie
in the
interiors
of our cones. This yields requirement (R1) given the sizes and angular
distances of the cones. Furthermore, any extended subtree is assigned slopes from a
single cone. This yields (R2).
−
For the example tree of Fig.2a,itsuffices to pick the 16 vectors that one gets from
reflecting the primitive vectors from the [0
,
2]
[0
,
2] grid. These vectors already fulfill
requirements (R1) and (R2). Hence, we did not have to apply the more involved slope
selection as described in Lemma 3. The resulting drawing isshowninFig.2b.
Every face in the drawing contains two leaves. The leaves are ordered by their ap-
pearance in some DFS-sequence
×
respecting some rooted combinatorial embedding
of
T
. For a face
f
, we call the leaf that comes first in
D
the
left leaf
and the other leaf
of
f
the
rightleaf
of
f
. The only exception is the face whose leaves are the first and
last child of
D
D
. Here we call the first vertex in
D
the right leaf and the last vertex in
D
the left leaf.
Lemma 4.
Let
u
be theleftleaf, andlet
v
be therightleafofa face of
T
.Further, let
w
be thelowest commonancestor of
u
and
v
.The above assignment of slope ranks
s
to
thetreeedges implies the following.
(a)Ifedge
e
1
is on the
w
-
u
pathandedge
e
2
is on the
w
-
v
path,then
s
(
e
1
)
<s
(
e
2
)
.
(b) The ordered sequence of edges on thepath
w
ₒ
u
is increasing in
s
(
·
)
.
(c) The ordered sequence of edges on thepath
w ₒ v
is decreasing in
s
(
·
)
.
The proof is omitted because of space constraints. We now prove the correctness of our
algorithm.
Theorem 1.
Givenanembedded tree with
n
vertices (noneofdegree 2), theinorder-
algorithm produces a strictly convex and crossing-free drawing with angularresolution
ʩ
(1
/n
)
onagrid of size
O
(
n
1
.
5
)
O
(
n
1
.
5
)
.The algorithm runsin
O
(
n
)
time.
×
Proof.
We first show that in the drawing no face is incident to an angle larger than
ˀ
.
Let
f
be a face, let
e
and
e
be two consecutive edges on the boundary of
f
,andlet
ʱ
be the angle formed by
e
and
e
in the interior of
f
.If
e
and
e
are incident to the root,
requirement (R1) implies
ʱ<ˀ
. If both edges contain the lowest common ancestor
of the leafs belonging to
f
,thenbyrequirement (R2) also
ʱ<ˀ
. In the remaining
case,
e
and
e
both lie on a path to the left leaf of
f
, or both lie on a path to the right