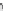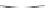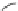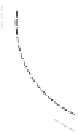Information Technology Reference
In-Depth Information
v
k
v
j
+1
p
1
p
0
v
1
μ
p
2
p
5
v
0
v
0
v
j
v
3
v
2
v
j−
1
p
3
p
4
(c)
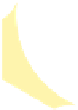
Fig. 6.
Constructing increasing-chord drawings of binary trees and cactuses in
(a)
(b)
2
H
For each such building block of the drawing consisting of a
K
1
,
3
insidearegular
hexagon with 90
ⓦ
angles, we add its copy mirrored at an arc of the hexagon containing
a leaf node of the tree constructed so far. For example, in the first iteration, we add
three copies of
mirrored at
p
0
p
1
,
p
2
p
3
and
p
4
p
5
, respectively, and the corresponding
inscribed
K
1
,
3
subtrees. The construction after two iterations is shown in Fig.6b.This
process can be continued infinitely to construct a drawing
ʓ
∞
of the infinite binary tree.
However, we stop after we have completed
ʓ
for the tree
T
.
We now show that
ʓ
∞
(and thusalso
ʓ
) has the desired properties. Due to isometries
and the aforementioned sufficient condition, it suffices to consider edge
e
=
v
0
v
1
and
show that a normal on
e
does not cross
ʓ
∞
in another point. To see this, consider Fig.6a.
Due to the choice of the angles of
, all the other hexagonal tiles of
ʓ
∞
are contained in
one of the three bluequadrangular regions
l
v
i
p
2
i−
2
),
i
=1
,
2
,
3.
Thus, the regions
l
v
1
p
1
and
l
v
1
p
0
(gray) contain no point of
ʓ
∞
. Therefore, since each
normal on
v
0
v
1
is contained in the “slab”
D
i
:=
l
v
0
v
i
\
(
l
v
i
p
2
i−
1
∪
l
v
1
v
0
) bounded by the diameter
through
p
2
,p
5
and the line through
p
0
,p
1
(dashed) and is parallel to both of these lines,
it contains no other point of
ʓ
∞
.
(
l
v
0
v
1
∪
\
We note that our proof is similar in spirit to the one by Kleinberg [12], who also used
tilingsof
2
.
As in the Euclidean case, it can be easily shown that if a tree
T
contains a node
v
of degree 4, it has a self-approaching drawing in
2
to prove that any tree has a greedy drawing in
H
H
2
if and only if
T
is a subdivision
of
K
1
,
4
(apply an isometry, such that
v
is in the origin of
D
). This completely charac-
terizes the trees admitting a self-approaching drawing in
H
2
.Further, it is known that
every binary cactus and, therefore, every 3-connected planar graph has a binary span-
ning tree [5, 13].
Corollary 2.
(i)
Atree
T
has an increasing-chord drawing in
H
2
if andonly if
T
either has maximum degree 3 or is a subdivision of
K
1
,
4
.
(ii)
Every binary cactus and,
therefore, every 3-connected planar graphhas an increasing-chord drawing in
H
2
.
H
2
; see the example in
Theorem 2. We use the above construction to produce
planar
self-approaching drawings
of binary cactuses in
R
Again, note that this is not the case for binary cactuses in
2
. We show how to choose a spanning tree and angles at vertices
of degree 2, such that non-tree edges can be added withoutintroducing crossings; see
Fig.6cforasketchandthefull version [15] for the proof.
H
2
.
Corollary 3.
Every binary cactus has a planarincreasing-chord drawing in
H