Information Technology Reference
In-Depth Information
c
l
a
r
a
l
c
r
c
a
a
c
a
c
r
s
2
s
1
a
c
r
r
r
(a)
(b)
(c)
Fig. 4.
Showing the contradiction in Theorem 2
(90
ⓦ
−
ʵ
)+90
ⓦ
.Nowlet
b
2
lie to the right of ray(
r
2
,c
2
). Then,
b
2
is above
c
2
c
1
,andit
(90
ⓦ
−
ʵ
)+90
ⓦ
.Since
ʵ<
22
.
5
ⓦ
, this contradicts
is
∠
r
2
c
2
b
2
=
∠
c
1
c
2
r
2
+
∠
c
1
c
2
b
2
≥
90
ⓦ
.Thus, by Lemma 4(iii),
Lemma 4(iii). Similarly,
∠
r
2
c
2
b
2
≥
∠
r
2
c
2
b
2
,
∠
r
2
c
2
b
2
∈
[90
ⓦ
,
90
ⓦ
+
ʵ
].Since
90
ⓦ
,
b
2
lies to the right of ray(
r
2
,a
2
) and to the left
of ray(
r
2
,c
2
). (If
b
2
lies to the left of both rays, it is
∠
a
2
b
2
c
2
≥
(
# »
a
2
b
2
,
# »
∠
a
2
b
2
c
2
=
∠
c
2
b
2
)
≤
2
ʵ<
90
ⓦ
.) (ii) Similarly, if a self-approaching
b
2
a
0
-path uses
c
2
instead of
a
2
,itis
∠
r
2
c
2
b
2
≥
180
ⓦ
−
ʵ
. The last part follows analogously.
From now on, let
μ
0
be the root block of
G
r
and
μ
1
,
μ
2
,
μ
3
its descendants such
that
r
(
μ
1
)=
c
0
,
r
(
μ
2
)=
a
1
,
r
(
μ
3
)
∈{
a
2
,c
2
}
;seeFig.3d.Light gray blocks are the
subject of Lemma 6(i), which shows that several ancestor roots lie inside a cone with
asmallangle. Dark gray blocks are the subject of Lemma 6(ii), which considers the
intersection of the cones corresponding to a pair of sibling blocks and shows that some
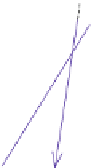
of their ancestor roots lie inside a narrow strip; see Fig. 4a for a sketch.
Lemma 6.
Let
μ
be a block in
G
c
2
withvertices
a
,
b
,
c
,
r
(
μ
)
.
(i)
Let
μ
havedepth 5
in
G
r
.Then,thecone
l
ba
∩
l
bc
contains
r
(
μ
)
,
r
(
ˀ
(
μ
))
,
r
(
ˀ
2
(
μ
))
and
r
(
ˀ
3
(
μ
))
.
(ii)
Let
μ
havedepth 4in
G
r
.There exist
u
in
G
a
and
v
in
G
c
of degree 4 and a strip
S
containing
r
(
μ
)
,
r
(
ˀ
(
μ
))
,
r
(
ˀ
2
(
μ
)) =
r
(
μ
2
)
,such that
u
and
v
lie on the different
boundaries of
S
.
Again, we consider two siblings and the intersection of their corresponding strips,
which forms a small diamond containing the root of the ancestor block; see Fig.4b,4c.
Lemma 7.
Consider block
μ
=
μ
3
containing
r
=
r
(
μ
)
,a,b,c
, andlet
r
ˀ
:=
r
(
ˀ
(
μ
3
))
.
It holds:
(i)
(1+2 tan
ʵ
)(tan
ʵ
)
2
cos
ʵ
(tan
ʵ
)
2
.
|
r
ˀ
r
|≤
(
|
ra
|
+
|
rc
|
)
;
(ii)
|
ra
|
,
|
rc
|≤|
rr
ˀ
|
22
.
5
ⓦ
, the two claims of Lemma 7 contradict each other. This concludes the
proof of Theorem 2.
For
ʵ
≤
4
Planar Increasing-Chord Drawings of 3-Trees
In this section, we show how to construct planar increasing-chord drawings of 3-trees.
We m a ke use of
Schnyder labelings
[20] and drawingsoftriangulations based on them.
For a plane triangulation
G
=(
V,E
) with external vertices
r, g, b
, its Schnyder label-
ing is an orientation and partition of the interior edges into three trees
T
r
,T
g
,T
b
(called