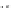Information Technology Reference
In-Depth Information
p
n−
1
p
n
=
q
d
p
3
p
2
p
1
=
p
Fig. 1.
A convex point set that is one-sided with respect to a directed straight line
d
is a point
ʱ
i
p
i
where
A
convex combination
of a set of points
P
=
{
p
1
,...,p
k
}
ʱ
i
=1and
ʱ
i
≥
H
P
of
P
is the set
of points that can be expressed as a convex combination of the points in
P
.A
convex
pointset
P
is such that no point is a convex combination of the others. Let
P
be a
convex point set and
d
be a directed straight line not orthogonal to any line throughtwo
points of
P
. Order the points in
P
as their projections appear on
d
; then, the
minimum
point
and the
maximum point
of
P
with respect to
d
are the first and the last point in
such an ordering. We say that
P
is
one-sided with respect to
d
if the minimumandthe
maximum point of
P
with respect to
d
are consecutive along the border of
0 for each 1
≤
i
≤
k
.The
convex hull
H
P
.See
Fig.1.A
one-sided convex pointset
is a convex point set that is one-sided with respect
to some directed straight line
d
. The proof of our first lemma shows an algorithm to
construct an increasing-chord planar graph spanning a one-sided convex point set.
Lemma 1.
Let
P
be any one-sided convex pointsetwith
n
points. There exists an
increasing-chord planar graph spanning
P
with
2
n
−
3
edges.
Proof.
Assume that
P
is one-sided with respect to the positive
x
-axis
x
.Such a
condition can be met after a suitable rotation of the Cartesian axes. Let
{
p
1
,p
2
,...,p
n
}
be the points in
P
, ordered as their projections appear on
x
.
We s h ow b y i n duction on
n
that an increasing-chord planar graph
G
spanning
P
exists, in which all the edges on the border of
H
P
are in
G
.If
n
=2then the graph
with a single edge
p
1
p
2
is an increasing-chord planar graph spanning
P
.Next,assume
that
n>
2 and let
p
j
be a point with largest
y
-coordinate in
P
(possibly
j
=1or
j
=
n
). Point set
Q
=
P
1
points. By induction, there exists an increasing-chord planar graph
G
spanning
Q
in
which all the edges on the border of
\{
p
j
}
is convex, one-sided with respect to
x
, and has
n
−
H
Q
are in
G
.Let
G
be the graph obtained by
adding vertex
p
j
and edges
p
j−
1
p
j
and
p
j
p
j
+1
to
G
.Wehavethat
G
is planar, given
that
G
is planar and that edges
p
j−
1
p
j
and
p
j
p
j
+1
are on the border of
H
P
.Further, all
the edges on the border of
H
P
are in
G
.Moreover,
G
contains an increasing-chord path
between every pair of points in
Q
,byinduction; also,
G
contains an increasing-chord
path between
p
j
and every point
p
i
in
Q
, as one of the two paths on the border of
H
P
connecting
p
j
and
p
i
is both
x
-and
y
-monotone, and hence increasing-chord by the
results in [2]. Finally,
G
is a maximal outerplanar graph, hence it has 2
n
−
3 edges.
The
Gabriel graph
of a point set
P
is the geometric graph that has an edge
pq
be-
tween two points
p
and
q
if and only if the closed disk whose diameter is
pq
contains
no point of
P
in its interior or on its boundary. A
Gabriel triangulation
is a tri-
angulation that is the Gabriel graph of its point set
P
. We say that a point set
P
admits
\{
p,q
}