Information Technology Reference
In-Depth Information
(a)
(b)
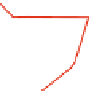
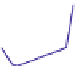
Fig. 3.
(a) An input for CST with
n
=10points and
k
=3colors. (b) An optimal solution with
minimum ink containing Steiner points.
If a shape
S
is convex, then there exists a minimum spanning tree on the given
point set such that every edge of the tree lies completely in
S
; non-convex shapes do
not necessarily admit such a spanning tree. Hence, the length of a shortest curve that
belongsto
S
and connects all the input points is an indicator of convexity of
S
.Inthe
following measure, we compare the length of such a curve (or equivalently, the amount
of “ink” needed to connect all the points) with the length of a minimum spanning tree
on the same point set; see Figs. 2(d)-2(e).
Minimum Ink.
Let
|
INK(
P
)
|
be the length of the shortest curve connecting all vertices
of
V
lying in
S
,andlet
|
MST(
P
)
|
be the length of the minimum spanning tree of
V
.
The measure is defined as
|
MST(
P
)
|
|
INK(
P
)
|
.Again, 1 indicates the best possible value(though,
it does not always correspond to a convex shape); smaller values are worse.
There are advantages and disadvantages of all of the proposed convexity measures, and
there are also many other ways to define convexity of shapes or polygons. In an attempt
to balance theoretical and practical considerations, we focus on visibility-based and the
ink-based measures. Similar ink-based criteria are used for constructing LineSets and
KelpDiagrams. By minimizing the ink needed for drawing, all of these techniques aim
to reduce visual clutter and increase the readability of the representation.
3.2
Algorithm for Ink Minimization
Here we study a problem motivated by computing contiguousregions with minimum
ink. The input consists of
n
points in the plane, and each point is associated with one of
k
colors. The CST (C
OLORED
S
PANNING
T
REES
) problem is to connect points of the
same color by mutually non-intersecting curves of shortest total length. In an optimal
solution each curve forms a tree spanning points of the corresponding color. The trees
may use additional (Steiner) points that do not belong to the original pointset; see Fig.3.
Computing an optimal solution for CST is
NP
-hard. This follows from the observa-
tion that the known
NP
-complete M
INIMUM
S
TEINER
T
REE
problem is a special case
of CST, in which the input consists of monochromatic points. Next we present a heuris-
tic for CST and prove that it is an approximation algorithm in the theoretical sense.
We refer to the minimum spanning and Steiner trees of a set of points
P
as MST(
P
)
and SMT(
P
), respectively; their lengths are denoted by
.
We use the Steiner ratio, denoted by
ˁ
, which is the supremum of the ratio of the length
of a minimum spanning tree to the length of a minimum Steiner tree. It is conjectured
that
ˁ
=
|
MST(
P
)
|
and
|
SMT(
P
)
|
2
√
3
≈
1
.
15,and
≈
1
.
21 is the best-known upper bound on
ˁ
[5].