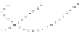Clustered Planarity Testing Revisited - Graph Drawing - page 435

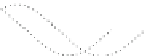
a standing cylinder taking the angle as the parameter. The vertices of the cycle are at

i

rk +1 ˀ, 0 ,where i =0 ,...,rk

2 k 2 ki +1

− 1, and the lines separating clusters at

rk +1 ˀ ,for

i =0 ,...r −

1,seeFig.2.By[7],foranyclustered drawing of any of ourexamples,
the curve representing the cycle has winding number k around p , and therefore, it is not
c-planar when k> 1.

13 10 7 4 1 14 11 8 5 2 15 12 9 6 3 13 10 7 4 1

Fig. 2. Acounter-example to the variant of the Hanani-Tutte theorem with parameters r =3
and k =5, and hence, the underlyinggraph is a cycle on 15 vertices. The vertices are labeled
by positive integers in correspondence with their appearance on the cycle. The leftmost and the
rightmost cluster need to be identified in the actual cylindrical drawing.

5 Small Faces

This section reproves a result of Di Battista and Frati [11] that c-planarity can be de-
cided in polynomial time for embedded flat clustered graphs if all faces are incident
to at most five vertices. Our approach seems quite different from theirs, as we use (a
corollary of) the matroid intersection theorem [12,27], which says that the largest com-
mon independent set of two matroids can be found in polynomial time. See e.g. [29] for
further references.
In this section, we will use a shorthand notation ( G, T ) instead of ( ( G ) ,T ) for an

embedded clustered graph. Let ( G, T ) be a embedded flat clustered graph. A saturator

D

of ( G, T ) is a subset F of 2 disjoint from E ( G ) such that ( G ∪F,T ) is planar, every
cluster of ( G ∪ F,T ) is connected, and the edges in F can be embedded so that every
cluster of ( G ∪ F,T ) is in the outer face of every other cluster. We have the following
simple fact regarding saturators already observed by Feng, Cohen and Eades [14].

Observation 1. An embedded flatclustered graph ( G, T ) is c-planarifandonly if
( G, T ) has a saturator.

In order to model our problem by matroids we need to avoid two saturating edges
in one face coming from two different clusters (even if they do not cross). In general,
this is not possible if the face is not a simple cycle. Thus, we first augment the graph by
adding some edges inside the faces.

Lemma 3. An embedded flatclustered graph ( G, T ) , all of whose faces are incidentto
at most five vertices, can be augmented byadding edges into an embedded flatclustered
graph ( G ,T ) such that ( G, T ) is c-planarifandonly if ( G ,T ) is c-planar, andthe
following holds for ( G ,T ) .If ( G ,T ) is c-planarthen ( G ,T ) has a saturator F
whose edges can be embedded so thateach face of G contains at most oneedgeof F .