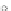Information Technology Reference
In-Depth Information
the most prominent [5] of such planarity notions. Roughly speaking, an instance of this
problem is a graph whose vertices are partitioned into clusters. The question is, then,
whether the graph can be drawn in the plane so that the vertices from the same clus-
ter belong to the same region and no edge crosses the boundary of a particular region
more than once. The aim of the present work is to offer novel perspectives on clustered
planarity, which seem to be worth pursuing in order to better our understanding of the
problem.
More precisely, a
clustered graph
is a pair (
G, T
) where
G
=(
V,E
) is a graph and
T
is a rooted tree whose set of leaves is the set of vertices of
G
. The non-leaf vertices of
T
represent the clusters. For
ʽ
V
(
T
),let
T
ʽ
denote the subtree of
T
rooted at
ʽ
.The
cluster
V
(
ʽ
) is the set of leaves of
T
ʽ
.Thesubgraph of
G
induced by
V
(
ʽ
) is denoted
by
G
(
ʽ
).
A
drawing
of
G
is a representation of
G
in the plane where every vertex is repre-
sented by a unique point and every edge
e
=
uv
is represented by a simple arc joining
the two points that represent
u
and
v
. If it leads to no confusion, we do not distinguish
between a vertex or an edge and its representation in the drawing and we use the words
“vertex” and “edge” in both contexts. We assume that in a drawing no edge passes
throughavertex,notwoedges touch and every pair of edges cross in finitely many
points. A drawing of a graph is an
embedding
if no two edges cross.
Aclustered graph (
G, T
) is
clustered planar
(or briefly
c-planar
)if
G
has an embed-
ding in the plane such that
∈
(i) for every
ʽ ∈ V
(
T
), there is a topological disc
d
(
ʽ
) containing all the leaves of
T
ʽ
and no other vertices of
G
such that if
μ ∈ T
ʽ
then
d
(
μ
)
ↆ d
(
ʽ
);
(ii) if
μ
1
and
μ
2
are children of
ʽ
in
T
,then
d
(
μ
1
) and
d
(
μ
2
) are internally disjoint;
(iii) every edgeof
G
intersects the boundary of
d
(
ʽ
) at most once for every
ʽ
∈
V
(
T
).
A
clustered drawing (or embedding)
of a clustered graph (
G, T
) is a drawing (or em-
bedding, respectively) of
G
satisfying (i)-(iii). See Fig. 1 for an illustration. We will be
using the word “cluster” for both the topological disc
d
(
ʽ
) and the subset of vertices
V
(
ʽ
).
(
G
,
T
)
T
(a)
(b)
Fig. 1.
(a) A clustered embedding of a clustered graph (
G, T
) and its tree
T
;(b)Aclustered
graph with two non-trivial clusters, which is not c-planar
The notion of clustered planarity was introduced in the work of Feng, Cohen and
Eades [13,14] under the name of c-planarity and a similar problem was considered