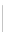Information Technology Reference
In-Depth Information
6
5
r
4
3
2
c
b
a
1
Fig. 3.
A graph that can be drawn on 6 rows, but not if edges must be
y
-monotone
3.2
y
-monotonicity
Thm. 1 used
y
-monotonicity of the poly-line drawing. One can show that
y
-
monotonicity is required.
Theorem 3.
The graph in Fig. 3 has a planar poly-line drawing on 6 rows, but
no planar y-monotone orthogonal drawing on 6 rows.
Proof.
(Sketch) Due to the
K
2
,
5
's between
r
and each of
, vertices
a,b,c
must all be in the same row. This makes it impossible to draw cycle
a
{
a,b,c
}
−
b
−
c
−
a
with
y
-monotone curves.
Corollary 2.
There exists a planar graph with a planar poly-line drawing on 6
rows that has no planar straight-line drawing on 6 rows.
Proof.
If the graph in Fig. 3 had a straight-line drawing on 6 rows, then by
Thm. 5 (below) it would have a
y
-monotone orthogonal drawing on 6 rows,
contradicting Thm. 3.
4F tD awings
This section is devoted to drawings where vertices are horizontal segments or
points, and in particular aims to show that poly-line drawings are equivalent
to flat orthogonal drawings as far as height is concerned. Note that neither of
these implications is trivial: A poly-line drawing allows slanted line segments
while a flat orthogonal drawing does not, and a flat orthogonal drawing allows
horizontal segments for vertices while a poly-line drawing does not.
Theorem 4.
Any planar flat orthogonal drawing ʓ can be transformed into a
planar poly-line drawing ʓ
of the same height that preserves y-coordinates and
left-to-right orders. ʓ
has no more width than ʓ. Moreover, if ʓ is y-monotone
then so is ʓ
.
Proof.
First insert
pseudo-vertices
obtained by subdividing edges at bends and
whenever a vertical segment of an edge crosses a row. Any pseudo-vertex is
located on a grid-point since the edge segment was vertical, so this does not