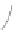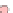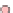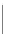Information Technology Reference
In-Depth Information
9
V
14
13
9
8
H
V
9
H
1
3
9
7
13
H
V
V
V
V
V
V
H
V
V
3
13
H
11
V
H
H
H
1
8
13
10
V
6
H
12
11
H
H
H
15
12
6
H
11
12
15
H
10
H
V
V
7
V
5
14
V
V
14
H
H
15
V
14
V
V
H
10
10
H
V
6
4
V
V
H
H
V
V
V
7
11
V
H
15
4
4
H
2
4
5
H
H
2
H
H
H
H
H
2
V
6
V
V
V
V
V
V
V
V
V
H
H
V
H
7
H
H
3
1
5
1
3
2
5
8
12
8
H
(a)
(b)
(c)
(d)
Fig. 1.
(a) An HV-graph. (b) An HV-drawing of the HV-graph of Fig. 1(a). (c) An HV-graph that
does not admit an HV-drawing. (d) A rectilinear orthogonal drawing of the graph of Fig. 1(c).
fixed embedding setting
, i.e., when the rectilinear orthogonal representation must pre-
serve a planar embedding of
G
given as part of the input [18]. The rectilinear planarity
testing problem is however NP-complete in the
variable embedding setting
, i.e., over
all planar embeddingsof
G
[11]. Polynomial-time solutions exist if
G
is a biconnected
series-parallel graph or if
G
has maximum vertex-degree three (see, e.g., [7,16,20]).
The rectilinear planarity testing problem is a classical subject of investigation in the
graph drawing literature, and it can be regarded as a special case of the bend mini-
mization problem for orthogonal drawings, probably one of the most explored topics in
the field (see, e.g., [1,2,7,10,14,15,18]). Direction constrained versions of the rectilinear
planarity testing problem also have a long tradition in the literature. An example is when
every edgeof
G
is labeled 'Up”, or “Down”, or “Left”, or “Right” and one wants to test
whether
G
has a rectlinear drawing where every edge has a direction consistent with its
label (see, e.g. [12,19]); the 3D version of this problem has also been studied [5,6,8].
In this paper we study another direction constrained version of the rectilinear pla-
narity testing problem that has been receiving increasing interest. An
HV-restricted
planar graph
(
HV-graph
for short)
G
=(
V,E
) is a planar graph with vertex-degree
at most foursuch that each edge is labeled either H (horizontal) or V (vertical).
Denote by
E
H
ↂ E
and
E
V
ↆ E
the subsets of H- and V-labeled edges, respec-
tively. An
HV-drawing
of
G
is a rectilinear orthogonal drawing of
G
such that each
edge
e
E
V
) corresponds to an orthogonal (resp. vertical) segment.
An
HV-realization
of
G
is a rectilinear orthogonal representation
∈
E
H
(resp.
e
∈
H
of
G
such that
every drawing of
is an HV-drawing of
G
, up to a rotation of 90 degrees. The
HV-rectilinearplanarity testing
problem asks whether an HV-graph admits an HV-
realization. Figure1(b)showsanHV-drawing of the HV-graph in Fig. 1 (a). Fig-
ure1(c)showsanHV-graph that does not admit HV-realizations, although it admits
a rectilinear orthogonal drawing (Fig. 1 (d)).
Manuch
et al.
[13] ask what is the time complexity of HV-rectilinear planarity test-
ing both in the fixed and in the variable embedding setting.Durocher
et al.
[9] describe
a polynomial-time testing algorithm in the fixed embedding setting; for the variable
embedding setting they present a quadratic-time testing algorithm for biconnected out-
erplanar graphs of vertex-degree at most three. The authors leave as open problem both
to characterize the outerplanar HV-graphs that admit an HV-realization and to establish
H