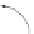Information Technology Reference
In-Depth Information
v
i
v
i
μ
e
μ
e
3
2
2
e
e
v
j
v
j
v
i
v
i
+1
v
i
v
i
+1
e
2
v
G
k−
1
v
G
k−
1
v
j
v
j
G
k−
1
G
k−
1
G
k−
1
(c)
G
k−
1
(d)
(a)
(b)
(e)
(f)
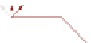
Fig. 6.
(a) Virtual edge
e
=(
v
i
,v
i
+1
) connecting two consecutive vertices of a chain. At both
endpoints the drawing of
μ
e
requires two ports. (b) Replacing
e
in (a) with the corresponding
drawing of the child
μ
e
. (c) Example of an edge
e
=(
v
j
,v
j
) that requires three ports at
v
j
and
two at
v
j
. (d) Inserting the drawing of
μ
e
into (c) with
v
j
being fixed and
v
j
forming a nose.
(e) Reserving ports for the nested edges. A single port for a real edge is reserved and then two
ports for the virtual edgee=(
v
i
,v
). (f) Final layout after inserting the drawing of
μ
e
.
Theorem 5.
Givenabiconnected 5-planar graph
G
, wecan compute in
O
(
n
2
)
time an
octilineardrawing of
G
withat most onebend per edge.
Proof.
The ability to rotate and scale suffices to extend the result from 4-planar to 5-
planar at the expense of the area. Similar to the 4-planar case, computing
T
takes linear
time. Hence, the overall runtime is governed by the triconnected algorithm.
The Simply Connected Case.
Due to lack of space, we outline the differences in
comparison to the 4-planar case in [1]. Here, we simply state the main theorem.
Theorem 6.
Givenaconnected 5-planar graph
G
, wecan compute in
O
(
n
2
)
time an
octilineardrawing of
G
withat most onebend per edge.
4
A Note on Octilinear Drawings of 6-Planar Graphs
In this section, we show that it is not always possible to construct a planar octilinear
drawing of a given 6-planar graph with at most one bend per edge.
Theorem 7.
There exists an infinite class of 6-planar graphs which do not admit planar
octilineardrawings withat most onebend per edge.
Sketch of Proof.
Due to lack of space the detailed proof of this theorem is given in [1].
The main idea is to construct an infinite class of maximal 6-planar graphs, whose outer
face is always delimited by exactly three vertices, say
v,v
and
v
,such that
deg
(
v
)=
deg
(
v
)=6and 5
deg
(
v
)
6. Then, it is not difficult to prove that it is not feasible
to draw all edges incident to the outer face with at most one bend per edge.
≤
≤
5
Conclusions
We presented algorithms for the construction of planar octilinear drawings with at most
one bend per edge for 4- and 5-planar graphs. Our work raises several open problems:
(i) Is it possible to construct planar octilinear drawings of 4-planar (5-planar) graphs
with at most one bend per edgein
o
(
n
3
) (polynomial, resp.) area? (ii) Does any triangle-
free 6-planar graph admit a planar octilinear drawing with at most one bend per edge?
(iii) What is the number of necessary slopes for bendless drawingsof4-planar graphs?