Information Technology Reference
In-Depth Information
v
n
v
i
v
i
v
j
v
v
v
i
v
j
v
1
v
3
v
2
v
1
v
2
v
1
v
2
(a)
(b)
(c)
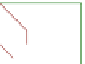
Fig. 4.
(a) Horizontal placement of a chain
P
k
=
{v
i
,...,v
j
}
.(b)Placement of a singleton
P
k
=
{v
i
}
of degree five. (c) Final layout (the shape of the dotted edges can be obtained by
extending the stubs until they intersect).
of degree 5, we have to deal with two additional
edges (called
nested
) that connect
v
i
with
G
k−
1
,say(
v
i
,v
) and (
v
i
,v
);seeFig.4b.
Such a pair of edges does not always allow vertex
v
i
to be placed along the next avail-
able horizontal grid line. A careful case analysis on the type of ports that are unoccupied
at
v
and
v
in conjunction with the fact that
G
k−
1
is horizontally stretchable shows that
we can find a feasible placement for
v
i
. Potential crossingsdue to the remaining edges
incident to
v
i
are eliminated by employing similar cuts to the ones presented in the 4-
planar case. So,
G
k
is planar. Also,
G
k
complies with the stretchability-invariant. The
last partition
P
m
=
In case of a singleton
P
k
=
{v
i
}
is treated in the same way, even if
v
n
can be incident to three
nested edges. Since
v
1
and
v
2
are along a common horizontal line, (
v
1
,v
2
) can be drawn
using two diagonal segments that form a bend pointing downwards; see Fig.4c. Note
that ouralgorithm may result in drawingsofsuper-polynomial area, as proven in [1].
{
v
n
}
Theorem 4.
Givenatriconnected 5-planar graph
G
, wecan compute in
O
(
n
2
)
time
an octilineardrawing of
G
withat most onebend per edge.
Proof.
We can no longer use the shifting method of Kant [11], since the
x
-and
y
-
coordinates are not independent. However, the computation of each cut can be done in
linear time, which implies that ourdrawing algorithm needs
O
(
n
2
) time in total.
The Biconnected Case.
For the 4-planar case we defined several invariants in order
to keep the area of the resulting drawings polynomial. Since we drop this requirement
now we can define a simpler new invariant for the biconnected 5-planar case. When
considering a node
μ
in
, then in the drawing of
G
per
μ
,
s
and
t
are horizontally aligned at the bottom of the drawing'sbounding box as in Fig.5a. If
an (
s, t
)-edge is present, it can be drawn at the bottom. An (
s, t
)-edge only occurs in the
pertinent graph of a P-node (and Q-node). We use the term
fixed
for a pole-node that is
not allowed to form a nose. We maintain the following properties throughtherecursive
construction process: In S- and R- nodes,
s
and
t
are not fixed. In P- and Q-nodes, only
one of them is fixed, say
s
.But as in the 4-planar case, we may swap their roles.
If
μ
is a P-node, then it has at most 4 children; one of them might be a Q-node, i.e., an
(
s, t
)-edge, which can be drawn at the bottom as a horizontal segment. Since P-nodes
are not adjacent to each other in
T
and its poles
P
μ
=
{
s, t
}
, the remaining children are S- or R-nodes. By our
invariant we may form noses enablingus to stack them as in Fig.5b.
T