Information Technology Reference
In-Depth Information
s
e
s
s
s
μ
1
s
μ
1
O
(
n
)
μ
2
t
t
t
μ
2
e
t
t
t
O
(
n
2
)
(a)
(b)
(c)
(d)
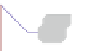
Fig. 2.
(a) Schematic view of the layoutrequirements. (b) Creating a nose at
t
.(c)FirstP-node
subcase withoutan(
s,t
)-edgebut
s
might be fixed in a child
μ
1
. (d) Second P-node subcase with
an (
s,t
)-edgewhere
t
might get fixed in a child
μ
2
.
not. But, if we relabel
s
and
t
such that
t
=
s
and
s
=
t
,then
deg
per
μ
(
s
)=1and
deg
per
μ
(
t
)=2.ByIP-2, we can create a drawing where both
s
and
t
are not fixed and
located in the upper-left and lower-right corner of the drawing'sbounding box. After-
wards, we mirror the resulting layout vertically and horizontally to obtain one where
s
and
t
are in their respective corners and not fixed. For a non-fixed vertex, we introduce
an operation referred to as forming or creating a
nose
;seeFig.2b, where
t
has been
moved downwards at the cost of a bend. As a result, its west port is no longer occupied.
First consider the case where
μ
is a P-node. If there is no (
s, t
)-edge, then we draw
the children of
μ
from top to bottom such that a possible child in which
s
is fixed, is
drawn topmost (see
μ
1
in Fig.2c). If there is an (
s, t
)-edge, then we draw it at the top
and afterwards the remaining children of
μ
(see Fig.2d). This is possible only if
s
is
not fixed in any of the other children. Let
μ
be such a potential child where
s
is fixed,
i.e.,
deg
pert
μ
(
s
)=2,andthus, the only child that remains to be drawn. Here, we use
the property of interchangeability to “unfix”
s
in
μ
.Asaresult
s
can form a nose,
whereas
t
may now be fixed in
μ
when
deg
pert
μ
(
t
)=2holds, as in Fig.2d. However,
then
deg
per
μ
(
t
)=3follows. Notice that the presence of an (
s, t
)-edge implies that the
parent of
μ
is not the root of
T
, since this would induce a pair of parallel edges. Hence,
by IP-2 we are allowed to fix
t
in
μ
. Port assignment and area requirements comply in
both cases with our invariant properties.
In the case where
μ
is an S-node, we place the drawings of its children, say
μ
1
,...,μ
in a “diagonal manner” such that their corners touch as in Fig.3a. In case of Q-nodes
being involved, we draw their edges as horizontal segments (see, e.g., (
v
3
,v
4
) in Fig.3a).
s
and
t
inherit their port assignment and pertinent degree from
μ
1
and
μ
, respectively.
So,
s
(
t
,resp.)isfixedin
μ
,ifitisfixedin
μ
1
(
μ
,resp.).ByIP-2,
t
is not allowed to
be fixed in the case where the parent of
μ
is the root of
. However, from Lemma 2 we
can choose the root such that
t
is not fixed in that case, and thus, complies with IP-2.
Since we only concatenated the drawings of the children, IP-1 and IP-3 are satisfied.
For the case where
μ
is an R-node with poles
T
, we follow the idea of the
triconnected algorithm and describe only the required modifications. We assume the
worst case where no child of
μ
is a Q-node. Let
μ
uv
be the child that is represented by
the virtual edge (
u,v
)
P
μ
=
{
s, t
}
E
ske
μ
.Due to Lemma 1,
deg
pert
2 and
deg
pert
2
holds. By IP-2 we may assume that either
u
or
v
is fixed in
μ
uv
and choose the first
partition in the canonical ordering to be
P
0
=
∈
μ
uv
(
u
)
≤
μ
uv
(
v
)
≤
{
s, t
}
.
with two neighbors
v
i
and
v
j
in
G
k−
1
,
we have to replace two types of edges with the drawings of the corresponding children:
In case of a chain, say
P
k
=
{
v
i
,...,v
j
}