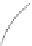Information Technology Reference
In-Depth Information
let
˃
=(
v
1
,v
2
, ..., v
n
) be an ordering of all the vertices of
G
.Then
G
k
,where
2
v
k
,and
P
k
is the path
(while walking clockwise) on the outer face of
G
k
that starts at
v
1
and ends at
v
2
. The vertex-ordering
˃
is called a
canonical ordering
[9] with respect to the
outer edge (
v
1
,v
2
)ifforeach
k
,3
≤
k
≤
n
, is the subgraph of
G
induced by
v
1
∪
v
2
∪
...
∪
n
, the following conditions are satisfied:
(a)
G
k
is 2-connected and internally triangulated. (b) If
k
≤
k
≤
n
,then
v
k
is an
outer vertex of
G
k
and the neighbors of
v
k
in
G
k−
1
appears consecutively on
P
k−
1
. Figures 3(a)-(b) illustrate an example.
For some
j
,where3
≤
n
,let
P
j
be the path
w
1
(=
v
1
)
,...,w
l
,v
k
(=
w
l
+1
)
,w
r
,...,w
t
(=
v
2
). We call the edges (
w
l
,v
j
)and(
v
j
,w
r
)the
l-edge
and
the
r-edge
of
v
j
, respectively. The other edges incident to
v
j
in
G
j
are called the
m-edges
of
v
j
. For example, in Figure 3(c), the edges (
v
6
,v
4
)
,
(
v
6
,v
5
), and (
v
3
,v
6
)
are the
l
-,
r
-and
m
-edges of
v
6
, respectively. By
d
l
(
v
)
,d
r
(
v
)and
d
m
(
v
)wedenote
the number of
l
,
r
and
m
-edges that are incoming to
v
, e.g.,
d
l
(
v
6
)=0
,d
r
(
v
6
)=1
and
d
m
(
v
6
)=1.
Let
E
m
be the set of all
m
-edges in
G
. Then the graph
T
m
induced by the edges
in
E
m
is a tree with root
v
n
. Similarly, the graph
T
l
induced by all
l
-edges except
(
v
1
,v
n
) is a tree rooted at
v
1
(Figure 3(d)), and the graph
T
r
induced by all
r
-
edges except (
v
2
,v
n
) is a tree rooted at
v
2
. These three trees form the
Schnyder
realizer
[17] of
G
. A Schnyder realizer is called a
minimum realizer
if all the
cyclic inner faces are oriented clockwise. By
Δ
0
we denote the number of cyclic
inner faces in the minimum realizer [21]. If
≤
j
≤
is a minimum Schnyder
realizer of
G
,thenwehave
leaf
(
T
l
)+
leaf
(
T
r
)+
leaf
(
T
m
)=2
n
{
T
l
,T
r
,T
m
}
−
5
−
Δ
0
[3].
Hence we can observe the following property.
Remark 1.
Let
{
T
l
,T
r
,T
m
}
be a minimum Schnyder realizer of an n-vertex
triangulation. Then
min
{
leaf
(
T
l
)+
leaf
(
T
r
)
,
leaf
(
T
l
)+
leaf
(
T
m
)
,
leaf
(
T
r
)+
leaf
(
T
m
)
}≤
(4
n
−
2
Δ
0
−
10)
/
3.
Anon-rootvertexin
T
l
is called a
primary vertex of T
l
if it is the first child of
its parent in the clockwise order. Similarly, a non-root vertex in
T
r
is a
primary
vertex of T
r
if it is the first child of its parent in the anticlockwise order. We now
have the following lemma, whose proof is omitted due to space constraints.
Lemma 1.
Let n
l
and n
r
be the nonprimary vertices in T
l
and T
r
, respectively.
Then n
l
+
n
r
≤
leaf
(
T
l
)+
leaf
(
T
r
).
v
9
v
9
v
8
v
8
v
8
v
7
v
6
v
6
v
6
v
6
v
7
v
7
v
4
v
4
v
4
v
5
v
4
v
5
v
5
v
5
v
3
v
3
v
3
v
3
v
1
v
1
v
2
v
1
v
2
v
2
v
1
v
2
(a)
(b)
(d)
(c)
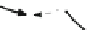
Fig. 3.
(a) A canonical ordering of a plane triangulation
G
.(b)
G
6
.(c)The
l
-,
r
-and
m
- edges are shown in dashed, bold-solid, and thin-solid edges respectively. (d)
T
l
.