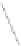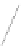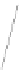Information Technology Reference
In-Depth Information
4 Morphing to Change Weight Distributions
Lemma 4.
(proof in the long version) Let
T
be a planar triangulation and let
S
be a Schnyder wood of
T
. Consider two weight distributions
w
and
w
on
the faces of
T
, and denote by
ʓ
and
ʓ
the weighted Schnyder drawings of
T
obtained from
w
and
w
respectively. Then the linear morph
ʓ,ʓ
is planar.
5 Morphing to Flip a Facial Triangle
In this section we prove that the linear morph from one Schnyder drawing to
another one, obtained by flipping a cyclically oriented face and keeping the same
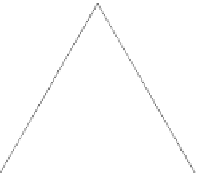
weight distribution, preserves planarity. See Figure 2. We begin by showing how
the regions for each vertex change during such a flip and then we use this to
show how the coordinates change.
a
1
a
1
a
1
a
3
a
2
a
3
a
2
a
3
a
2
Fig. 2. Snapshots from a linear morph defined by a flip of the shaded face at times
t
=0,
t
=0
.
5 and
t
=1
.
The trajectory of rectangular shaped vertices is parallel to
a
2
a
3
. Similar properties hold for triangular and pentagonal shaped vertices.
Let
S
and
S
be Schnyder woods of triangulation
T
that differ by a flip on
face
xyz
oriented counterclockwise in
S
with (
x, y
) of colour 1. Let (
v
1
,v
2
,v
3
)
and (
v
1
,v
2
,v
3
) be the coordinates of vertex
v
in the weighted Schnyder drawings
from
S
and
S
respectively with respect to weight distribution
w
. For an interior
edge
pq
of
T
,let
Δ
i
(
pq
) be the set of faces in the region bounded by
pq
and the
paths
P
i
(
p
) and
P
i
(
q
) in
S
, and we define
ʴ
i
(
pq
) to be the weight of that region,
i.e.,
ʴ
i
(
pq
)=
f∈ʔ
i
(
pq
)
w
(
f
).Weusenotation
P
i
(
v
)
,R
i
(
v
),and
D
i
(
v
) as defined
in Section 2 and
Δ
i
(
pq
) as above and add primes to denote the corresponding
structures in
S
. Let us begin by identifying properties of
S
and
S
. The following
two lemmas are proved formally in the long version.
Lemma 5.
The following conditions hold (see Figure 3):
1.
R
1
(
x
)=
R
1
(
x
)
,
R
3
(
y
)=
R
3
(
y
)
and
R
2
(
z
)=
R
2
(
z
)
.
2.
R
2
(
x
)=
R
2
(
x
)
)
,R
3
(
x
)=
R
3
(
x
)
\
(
Δ
1
(
yz
)
∪{
f
}
∪
(
Δ
1
(
yz
)
∪{
f
}
)
and similarly
for
y
and
z
.