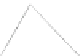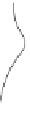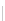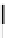Information Technology Reference
In-Depth Information
(a)
(b)
(c)
Fig. 4.
Illustration for the proof of Lemma 2. (a) Instance (
V,E,γ,T
) with flat hierarchy con-
taining clusters
μ
,
μ
,and
μ
ⓦ
. (b) Insertion of dummy vertices in (
V,E,γ,T
) to obtain
(
V
,E
,γ
,T
). (c) Level-connected instance (
V
∗
,E
∗
,γ
∗
,T
∗
) obtained from (
V
,E
,γ
,T
).
2
)
-time algorithm that decides whether a proper
instance
(
V,E,ʳ,T
)
of
T
-L
EVEL
P
LANARITY
is
Theorem 3.
There exists an
O
(
|V |
T
-level planar.
Proof:
The statement follows from Lemma 1 and from the existence of a quadratic-time
algorithm [7] that decides whether an instance
of SEFE-2 such that
G
1
and
G
2
are 2-connected and the common graph
G
∩
is connected admits a SEFE.
G
1
,
G
2
3.2
C
LUSTERED
-L
EVEL
P
LANARITY
In the following we show how to test in polynomial time the existence of a cl-planar
drawing for a proper instance (
V,E,ʳ,T
) of CL-P
LANARITY
.
A proper cl-graph (
V,E,ʳ,T
) is
μ
-connected between twolevels
V
i
and
V
i
+1
if
there exist two vertices
u
∈
V
μ
∩
V
i
and
v
∈
V
μ
∩
V
i
+1
such that edge (
u,v
)
∈
E
.For
acluster
μ
∈
T
,let
ʳ
min
(
μ
)=min
{
i
|
V
i
∩
V
μ
=
∅}
and let
ʳ
max
(
μ
)=max
{
i
|
V
i
∩
V
μ
. A proper cl-graph (
V,E,ʳ,T
) is
level-
μ
-connected
if it is
μ
-connected
between levels
V
i
and
V
i
+1
for each
i
=
ʳ
min
(
μ
)
,...,ʳ
max
(
μ
)
=
∅}
1. A proper cl-graph
(
V,E,ʳ,T
) is
level-connected
if it is
μ
-level-connected for each cluster
μ
−
T
.
Ourstrategy consists of first transforming a proper instance of CL-P
LANARITY
into
an equivalent level-connected instance, and then transforming such a level-connected
instance into an equivalent proper instance of
T
-L
EVEL
P
LANARITY
.
∈
Lemma 2.
Let
(
V,E,ʳ,T
)
be a proper instance of
CL-P
LANARITY
.An equivalent
level-connected instance
(
V
∗
,E
∗
,ʳ
∗
,T
∗
)
of
CL-P
LANARITY
whose size is quadratic
in thesizeof
(
V,E,ʳ,T
)
can be constructed in quadratic time.
Proof:
The construction of (
V
∗
,E
∗
,ʳ
∗
,T
∗
) consists of two steps. See Fig.4.
In the first step we turn (
V,E,ʳ,T
) into an equivalent instance (
V
,E
,ʳ
,T
).
Initialize
V
=
V
,
E
=
E
,and
T
=
T
. For each
i
=1
,...,k
and for each vertex
u
V
i
,set
ʳ
(
u
)=3(
i
∈
−
1) + 1. Then, for each
i
=1
,...,k
−
1, consider each edge
E
such that
ʳ
(
u
)=
i
and
ʳ
(
v
)=
i
+1; add two vertices
d
u
and
d
v
to
V
,and
replace (
u,v
) in
E
with edges (
u,d
u
), (
d
u
,d
v
),and(
d
v
,v
).Set
ʳ
(
d
u
)=3(
i
(
u,v
)
∈
1)+2
and
ʳ
(
d
v
)=3
i
. Finally, add
d
u
(
d
v
)to
T
as a child of the parent of
u
(of
v
)in
T
.
We prove that (
V
,E
,ʳ
,T
) is equivalent to (
V,E,ʳ,T
).
Suppose that (
V,E,ʳ,T
) admits a cl-planar drawing
ʓ
; a cl-planar drawing
ʓ
of
(
V
,E
,ʳ
,T
) is constructed as follows. Initialize
ʓ
=
ʓ
. Scale
ʓ
upbyafactor
of 3 and vertically translate it so that the vertices in
V
1
lie on line
y
=1.Afterthe
−