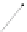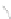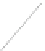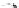Information Technology Reference
In-Depth Information
˄
μ
˄
μ
˄
μ
ʔ
(
t
μ
)
ʸ
ʔ(
s
ʷ
1
)
ʸ
ʔ(
s
ʷ
1
)
ʸ
ʔ
(
s
μ
)
ʸ
ʓ
ʷ
ʓ
ʷ
2
ʓ
ʷ
ʸ
ʓ
μ
ʓ
ʷ
1
ʓ
ʷ
1
s
μ
t
μ
s
μ
t
μ
s
μ
t
μ
ʸ
(a)
(b)
(c)
s
ʷ
5
s
ʷ
3
ʓ
ʷ
2
ʔ(
t
ʷ
3
)
ʸ
˄
μ
˄
μ
ʔ(
t
ʷ
3
)
ʸ
ˆ
ʓ
ʷ
3
g
j
g
3
ʓ
ʷ
3
s
μ
t
μ
ʓ
ʷ
1
ʓ
ʷ
1
g
2
2
ʸ
s
μ
ʓ
ʷ
2
s
μ
t
μ
t
μ
ʸ
ʸ
ʴx
2
ʴx
1
(d)
(e)
(f)
Fig. 3.
The planar drawing of the pertinent graph of: (a) a
P
-node with two children such that none
of them is a
Q
-node; (b) a
P
-node with three children, one of which is a
Q
-node; (c) a
P
-node
that is
AOS
in the outer 1-planar embedding of
G
;(d)an
R
-node; (e) an
R
∗
-node. (f) Illustration
for the proof of Lemma 10.
is
G
˕
=
G
μ
∪
replace
ʽ
with
˕
. The pertinent graph of
˕
G
ʷ
, and the reference edgeof
˕
is (
s
μ
,
t
μ
). We now explain how the different types of node are handled.
The proof of next lemmas are omitted. An illustration of how
ʓ
μ
is constructed is
shown in Figures 2(a) and 3.
Lemma 7.
Let
μ
be an S-node differentfrom
ʾ
.ThenG
μ
admits a straight-linedrawing
ʓ
μ
that respects Invariants
Ia.
,
Ib.
and
Ic
.
Lemma 8.
Let
μ
be aP-node differentfrom
ʾ
.ThenG
μ
admits a straight-linedrawing
ʓ
μ
that respects Invariants
Ia.
,
Ib.
and
Ic
.
Lemma 9.
Let
μ
be an R-node differentfrom
ʾ
.ThenG
μ
admits a straight-linedraw-
ing
ʓ
μ
that respects Invariants
Ia.
,
Ib.
and
Ic
.
be an R
∗
-node differentfrom
Lemma 10.
Let
μ
ʾ
.ThenG
μ
admits a straight-line
drawing
ʓ
μ
that respects Invariants
Ia.
,
Ib.
and
Ic
.
is an
R
∗
-node, it is obtained by merging an
R
-node
μ
and a
Q
-node
Proof.
Since
μ
μ
) of
μ
is isomorphic to
representing the edge (
s
μ
,
t
μ
).ByProperty 2, the skeleton
˃
(
μ
are
Q
-nodes. The two edges corresponding to these
Q
-nodes
do not share an end vertex and each one of them is incident to a distinct pole of
K
4
and two children of
μ
.Let
μ
;weassume that
ʷ
1
,
ʷ
2
,
ʷ
3
,
ʷ
4
,
and
ʷ
5
be the children of
ʷ
4
and
ʷ
5
are the two
Q
-
nodes. Also,
ʷ
6
that is a
Q
-node corresponding to the edge (
s
μ
,
t
μ
).
We a s sume that
s
μ
=
s
ʷ
1
=
s
ʷ
4
,
t
μ
=
t
ʷ
3
=
t
ʷ
5
,
t
ʷ
1
=
t
ʷ
2
=
s
ʷ
5
,and
t
ʷ
4
=
s
ʷ
2
=
s
ʷ
3
.
We construct a drawing of
G
μ
μ
has a sixth child
ʓ
ʷ
3
so that the
segment
s
ʷ
3
t
ʷ
3
uses the green slope
g
4ʔ
, and draw the edge associated with
as follows (see Figure 3(e)). We rotate
ʷ
5
as a
segment whose slope is the green slope (4
ʔ
−
ʔ
(
t
ʷ
3
))
ʸ
and whose length is such that
s
ʷ
5
is vertically aligned with
s
ʷ
3
.Werotate
ʓ
ʷ
2
so that the segment
s
ʷ
2
t
ʷ
2
uses the green
slope
g
2ʔ+1
=
2
. We then attach
ʓ
ʷ
2
,
ʓ
ʷ
3
,and
ʓ
ʷ
5
(possibly scaling some of them). We
draw the edge corresponding to
ʷ
6
with the horizontal slope
g
1
and stretch it so that