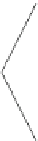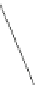Information Technology Reference
In-Depth Information
t
8
7
6
5
uv
w
4
3
2
s
s
1
Fig. 4.
A graph for which no bitonic
st
-
ordering exists for the given embedding
Fig. 5.
Running example with its bitonic
st
-
ordering and corresponding embedding
along the poles to turn a decreasing sequence into an increasing one. The latter changeis
caused by our invariant that only provides a decreasing sequence at
s
for the sake of an
easier maintainable invariant. In an actual implementation, this can easily be avoided by
mirroring the embedding twice, once before recursing on the corresponding child and
then afterwards. Thus, the resulting embedding is equivalent to the initial one. However,
for the P-node case it is not trivial and the question may arise if it is necessary in general,
or if one may always find a bitonic
st
-ordering for every edge when a fixed embedding
is given. To answer this question, we give a small counterexample.
Lemma 2.
Givenafixed embedding,there exist biconnected planar graphsthatdonot
admit a bitonic
st
-ordering for every edge.
Proof.
Consider the graph in Figure 4 and its embedding. The triangle consisting of
s
,
t
and
w
is attached to the source
s
via
s
. Clearly, in any feasible
st
-ordering
ˀ
(
u
)
<ˀ
(
t
)
and
ˀ
(
v
)
<ˀ
(
w
)
<ˀ
(
t
) must hold. Thus, the successor list
S
(
s
)=
of
s
as implied by the illustrated embedding is not bitonic with respect to
ˀ
, because it
follows that
ˀ
(
u
)
<ˀ
(
t
)
>ˀ
(
v
)
<ˀ
(
w
), which is neither bitonic increasing nor
decreasing.
{
u,t,v,w
}
Although this is a drawback, it is worth mentioning that in many approaches that employ
SPQR-trees for drawing purposes, implicit changes to the embedding are made anyway.
4
Applications
In the following, we present two simple applications of bitonic
st
-orderings. The results
are not new, but we believe that the bitonic
st
-ordering simplify things. By its nature,
it works out of the box for biconnected planar graphs and therefore no augmentation of
the inputisrequired. For both applications, we assume that a biconnected planar graph
G
=(
V,E
) with a bitonic
st
-ordering
ˀ
and the corresponding embedding is given. The
graph, its embedding and ordering displayed in Figure 5 serves as a running example.
We start with a classic problem: Straight-line drawings of biconnected graphs by
borrowing some ideas from Harel and Sardas [9]. They first describe an algorithm to
obtain a biconnected canonical ordering. Then a modification of the classic algorithm
of de Fraysseix, Pach and Pollack [3] is used to obtain a planar straight-line layout. We