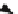Information Technology Reference
In-Depth Information
w
i−
1
∈ V
k
w
i−
1
w
i−
1
G
k
−
1
w
i
w
i
w
i
G
k−
1
v
v
v
w
i
+1
w
i
+1
w
i
+1
∈ V
k
(a)
(b)
(c)
Fig. 2.
(a) The initial situation at
v
with
S
(
v
)=
{...,w
i−
1
,w
i
,w
i
+1
,...}
.(b)
G
k−
1
with
k
=
ˀ
(
w
i−
1
) where
w
i−
1
hastobeintheouter face of
G
k−
1
.(c)
G
k
−
1
with
k<k
=
ˀ
(
w
i−
1
)
where
w
i
+1
hastobeintheouter face of
G
k
−
1
.
Lemma 1.
Every triconnected planar graph
G
=(
V,E
)
admits a bitonic
st
-ordering
for every
(
s, t
)
∈
E
.
Proof.
From its definition it is easy to see that a canonical ordering
V
1
∪···∪
V
K
can be transformed into an
st
-ordering
ˀ
. We start by describing the construction of
ˀ
and then show that it is indeed bitonic with respect to
ˀ
. Given an edge (
s, t
)
∈
E
,
s, s
}
we compute a canonical ordering
V
1
∪···∪
V
K
of
G
by choosing
V
1
=
{
and
with
s
being the vertex that precedes
t
in the clockwise order around
s
.
Notice that by definition of the canonical ordering,theedges (
s, t
) and (
s, s
) are on the
outer face. For the
st
-ordering
ˀ
we follow a simple principle that is sometimes referred
to as the vertex ordering of a canonical ordering:Regardless of
V
k
=
V
K
=
{
t
}
{
v
1
,...,v
m
}
with 1
≤
k
≤
K
being a chain or singleton, we choose
ˀ
for 1
≤
i
≤
m
such that
ˀ
(
v
i
)=
+
i
.
For the sake of notation we may refer to the partition of a vertex
v
|
V
1
|
+
···
+
|
V
k−
1
|
∈
V
k
with
ˀ
(
v
)=
k
. Notice that by construction of
ˀ
for all
u,v
V
with
ˀ
(
u
)
<ˀ
(
v
), it holds that
ˀ
(
u
)
<ˀ
(
v
). By definition of the canonical ordering,every
v ∈ V
k
with
k<K
has at least one neighbor
w
in
V
k
+1
∪···∪V
K
. It holds then that
ˀ
(
w
)
>ˀ
(
v
) and
as a result every
v
=
t
has at least one successor. In case
V
k
=
{v}
∈
(1
<k≤ K
)
is a singleton,
v
has at least two neighbors, say
c
l
and
c
r
,in
V
1
∪···∪
V
k−
1
with
ˀ
(
c
l
)
<ˀ
(
v
) and
ˀ
(
c
r
)
<ˀ
(
v
),thus
v
has at least two predecessors. The other case,
i.e.,
V
k
=
(
k>
1) is a chain, only
v
1
and
v
m
have one neighbor each, let
ussay
c
l
and
c
r
,in
V
1
∪···∪
{
v
1
,...,v
m
}
V
k
with
i>
1 it holds
that
ˀ
(
v
i−
1
)
<ˀ
(
v
i
). Hence, every
v
i
with
i<m
has exactly one predecessor while
v
m
has even two. Special attention must be paid to
V
1
=
V
k−
1
. However, for every
v
i
∈
s, s
}
since for this chain
no
c
l
and
c
r
exist. However, the predecessor of
s
is
s
and
s
itself does not require a
predecessor for
ˀ
being an
st
-ordering. Since all vertices
v
{
=
s
have predecessors the
order in
S
(
v
) is well-defined by considering them clockwise. For
s
we have to break
the cyclic order and set
S
(
s
)=
t
=
w
1
,w
2
,...,w
m−
1
,w
m
=
s
}
.
In order to prove that
ˀ
is a bitonic
st
-ordering, we first show that every successor
list obtained from
ˀ
is bitonic with respect to
ˀ
instead of
ˀ
.Todoso,assume to
the contrary that there exists a successor list
S
(
v
)=
{
{
w
1
,...,w
i
,...,w
m
}
of some
vertex
v
that is not bitonic with respect to
ˀ
, i.e., there is a
w
i
∈
S
(
v
) with 1
<