Information Technology Reference
In-Depth Information
Representations with Regular
3
k
-gons
6.2
We define the hexagonal grid
H
m,n
=(
V
H
,E
H
) as a subgraph of the square grid
S
m,n
:
H
m,n
:=
V
S
,E
S
\
(
v
i,j
,v
i
+1
,j
)
∈ E
S
(
i
+
j
) odd
.
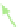
(a) (b)
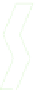
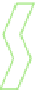
Fig. 8. (a)
Hexagonal Grid
H
5
,
5
; for thick edges, the moving sets are indicated by framed vertices
(b)
UTriPCR
ˆ
of
H
5
,
5
with illustration of modification step
Theorem 5.
Every subgraph of the hexagonal grid
H
m,n
has a UTriPCR.
Proof.
For the proof, we apply the already known technique. With
ʵ ∈
(0
,
1),aUTriPCR
of
H
m,n
is given by the following mapping and depicted in Figure 8:
ˆ
:
V
3
)
ₒP
R
(
⊧
⊨
4
2
h
+
ʵ
3
2
h
+
ʵ
2
h
−
6
h
+
4
−
1
if
i
+
j
even,
2
h
+
ʵ
2
h
+
4
−
h
+
ʵ
−
h
else.
Analyzing the shifts of the characteristic corner, it is not hard to verify that
ˆ
is a
UTriPCR of the triangular grid with contact size
cs
(
ˆ
)
4
2
h
+
ʵ
3
ˆ
(
v
i,j
)=
−
6
h
+
4
−
1
⊩
≥
−
ʵ
) and has moving
(1
space
sp
ˆ
(
u
)
,ˆ
(
v
)
,d
≥
ʵ
for (
u,v
)
∈
E
H
and direction vectors
d
parallel to the
sides of the triangles.
Indeed, two types of edges and direction vectors suffice: For
e
=(
v
i,j
,v
i,j
+1
),we
define direction
d
(
e
):=(
1
;
for
e
=(
v
i,j
,v
i
+1
,j
), we define direction
d
(
e
):=(1
,
0) and moving set
M
(
e
):=
{
−
2
,h
) and moving set
M
(
e
):=
{
v
i,k
∈
V
|
k>j
}
.Acrucial
property is that, again, the translation vector
d
(
e
) of an edge
e
is parallel to each of
the segments realizing contacts corresponding to edges of type (
u,v
)
v
i
+1+
k,j−k
∈
V
|
k
∈
[
m
−
i
]
}∪{
v
i
+1+
k,j−
1
−k
∈
V
|
k
∈
[
m
−
i
]
}
∈
E
\{
e
}
with
u
M
(
e
). Moreover,
d
(
e
) is not parallel to the segment realizing
this contact in
ˆ
. Note also that each edgebelongstoatmost
n
moving sets with the
same translation direction. Therefore, choosing
ʴ<
n
min
∈
M
(
e
) and
v/
∈
{
ʵ,
1
−
ʵ
}
the construction
analogous to Theorem 2 yields a UTriPCR for each subgraph
G
of
H
m,n
.
H
m,n
has a UPCR with regular
Corollary 4.
Every subgraph of the hexagonal grid
3
k
-gons,
k ≥
1
.
Proof.
Note that 3
k
-gons are pseudo-triangles with side length
s
k
:= tan(
3
k
)
h
. Choos-
ing
ʵ<
s
2
in the proof of Theorem 5, we obtain a UPCR
ˆ
for every subgraph
G
of
H
m,n
with
cs
(
ˆ
)
>
1
−
s
k
. With this, the claim follows directly from Theorem 5 and
Lemma 1.