Information Technology Reference
In-Depth Information
(
x, y
):=
b
∈
R
|
b
=
y
+
r
0
+
s
1
/
h
;
r, s
1
,
2
≥
0;
r
+
s
≤
1
.
For two touching polygons
S
u
,S
v
in the plane, we define the
size of contact
cs(
S
u
,S
v
)
by the length of its realizing segment; and for two touching
d
-dimensional polytopes
S
u
,S
v
, we define cs(
S
u
,S
v
) by the shortest edgelength of the (
d
(
x, y
):=
b
∈
R
|
b
=
y
+
r
0
+
s
1
/
2
h
;
r, s
2
≥
0;
r
+
s
≤
−
−
1)-dimensional
polytope realizing the contact. The
contact size
of a PCR
C
is given by cs(
C
):=
n
by a vector
t
n
min
{
cs(
S
u
,S
v
)
|
(
u,v
)
∈
E
}
.The
translation
of a set
S
∈
R
∈
R
is defined by the addition
S
+
t
:=
(
x
+
t
)
S
.The
space
sp(
S
u
,S
v
,d
)
n
∈
R
|
x
∈
of two objects
S
u
,S
v
in direction
d
is the maximum
ʴ
such that either object can
be translated by
ʴd
and they remain interiorly disjoint. Finally, [
n
]:=
∈
R
{
0
,...,n
}
.
2.1 Some Properties
We start with some basic properties of UPCRs. Clearly, PCRs in the plane may only
exist for planar graphs. Duetothecongruent objects, graphs with UPCR have bounded
maximumdegree and fulfill spatial constraints.
Observation 1.
Let
G
be agraphadmitting a UPCR with regular
n
-gons. Then,the
maximum degree is bounded by 6, i.e.
Δ
(
G
)
≤
6
.
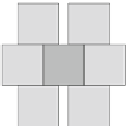
Fig. 1.
Examples of polygons and a cube with maximumnumber of neighbors in a UPCR
For triangles and squares, it is easy to see that the maximumdegree is 4 and 6,
respectively, see Figure 1. A general upper bound for regular polygons is given by
their
kissing number
, the maximal number of congruent copies a single polygon can be
touched by. Regular
n
-gons with
n
≥
5 have a kissing number of
≤
6, see [13, 14] for
further explanation.
Together with
ʩ
(
√
n
) polygons at the boundary of any (component of a) represen-
tation, this results in a low edge density: If a graph
G
on
n
vertices has a UPCR with
k
-gons, then the number of edges is
ʩ
(
√
n
). The analogousresult for unit
cube graphs has already been shown in [3]: For
G
=(
V,E
) with UCuPCR it holds that
Δ
(
G
)
≤
3
n
−
ʩ
(
n
3
).
We formulate spatial restrictions, duetothecongruent objects for
d
-cubes
:
Observation 2.
Let
G
be agraphwithaUPCR with
d
-cubes in
≤
14 and
|
E
|≤
7
n
−
d
.Then,everyvertex
R
has at most
(2
r
+1)
d
vertices in distance
r
.
This follows easily by comparing the available space in distance
≤
r
and the needed
space to place all congruent
d
-cubes. Consequently, there exist binary trees with no
UPCR with squares nor cubes.
For cubes, Bremner et al. [3], show that it is NP-complete to decide whether a graph
admits a UCuPCR. With the same ideas, we can show the analogousresult for squares:
≤