Java Reference
In-Depth Information
1
2
3
4
5
F
3
(X)
F
4
(X)
F
1
(X)
F
2
(X)
X
X
X
X
1
2
3
4
5
6
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
9
11
13
15
17
1
2
3
4
5
6
15
1
7
13
2
7
2
2
3
3
4
4
5
5
6
6
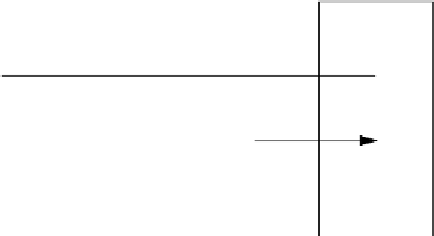
Figure17.7
An illustration of assigning functions to bins.
1
2
3
4
5
X
F
1
(X)
X
F
2
(X)
X
F
3
(X)
X
1
2
3
4
5
6
F
4
(X)
X
F
NEW
(X)
1
1
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
7
9
11
13
15
17
15
1
7
13
2
7
1
2
3
4
5
6
2
3
12
14
2
3
4
5
6
1
1
1
1
1
Figure17.8
Illustration for the argument that the number of integer functions is
uncountable.
any bin, as follows. Take the output value for input 1 from the function in the first
bin. Call this value F
1
(1). Add 1 to it, and assign the result as the output of a new
function for input value 1. Regardless of the remaining values assigned to our new
function, it must be different from the first function in the table, because the two
give different outputs for input 1. Now take the output value for 2 from the second
function in the table (known as F
2
(2)). Add 1 to this value and assign it as the
output for 2 in our new function. Thus, our new function must be different from
the function of Bin 2, because they will differ at least at the second value. Continue
in this manner, assigning F
new
(i) = F
i
(i) + 1 for all values i. Thus, the new
function must be different from any function F
i
at least at position i. This procedure
for constructing a new function not already in the table is called diagonalization.
Because the new function is different from every other function, it must not be in
the table. This is true no matter how we try to assign functions to bins, and so the
number of integer functions is uncountable. The significance of this is that not all
functions can possibly be assigned to programs, so there must be functions with no
corresponding program. Figure 17.8 illustrates this argument.