Java Reference
In-Depth Information
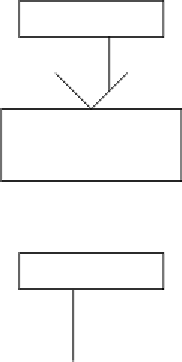
PROBLEM A:
I
TRANSFORM 1
I'
PROBLEM B
SLN'
TRANSFORM 2
SLN
Figure17.2
The general process for reduction shown as a “blackbox” diagram.
3. Transform SLN
0
to the solution of I, known as SLN. Note that SLN must in
fact be the correct solution for I for the reduction to be acceptable.
Figure 17.2 shows a graphical representation of the general reduction process,
showing the role of the two problems, and the two transformations. Figure 17.3
shows a similar diagram for the reduction of SORTING to PAIRING.
It is important to note that the reduction process does not give us an algorithm
for solving either problem by itself. It merely gives us a method for solving the first
problem given that we already have a solution to the second. More importantly for
the topics to be discussed in the remainder of this chapter, reduction gives us a way
to understand the bounds of one problem in terms of another. Specifically, given
efficient transformations, the upper bound of the first problem is at most the upper
bound of the second. Conversely, the lower bound of the second problem is at least
the lower bound of the first.
As a second example of reduction, consider the simple problem of multiplying
two n-digit numbers. The standard long-hand method for multiplication is to mul-
tiply the last digit of the first number by the second number (taking (n) time),
multiply the second digit of the first number by the second number (again taking
(n) time), and so on for each of the n digits of the first number. Finally, the in-
termediate results are added together. Note that adding two numbers of length M
and N can easily be done in (M +N) time. Because each digit of the first number