Java Reference
In-Depth Information
i
i
−1
1
−1
1
−i
−i
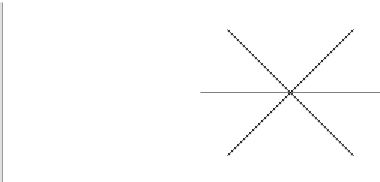
Figure16.6
Examples of the 4th and 8th roots of unity.
The idea is that there is a row for each root (row i for z
i
) while the columns corre-
spond to the power of the exponent of the x value in the polynomial. For example,
when n = 4 we have z = i. Thus, the A
z
array appears as follows.
1 1 1 1
1 i 1 i
1 1 1 1
1 i 1
A
z
=
i
Let a = [a
0
;a
1
;:::;a
n1
]
T
be a vector that stores the coefficients for the polyno-
mial being evaluated. We can then do the calculations to evaluate the polynomial
at the nth roots of unity by multiplying the A
z
matrix by the coefficient vector. The
resulting vector F
z
is called the Discrete Fourier Transform for the polynomial.
F
z
= A
z
a = b:
n1
X
a
k
z
ik
:
b
i
=
k=0
When n = 8, then z =
p
i, since
p
i
8
= 1. So, the corresponding matrix is as
follows.
1
1
1
1
1
1
1
1
p
i
i
p
i 1
p
i i i
p
i
1
i
1
i
1
i
1
i
1
i
i
p
i i
p
i 1 i
p
i
i
p
i
1
A
z
=
1
1
1
1
1
1
1
1
1
p
i
i i
p
i 1
p
i i
i
p
i
1
i
1
i
1
i
1
i
1 i
p
i i
p
i 1
i
p
i
p
i
i
We still have two problems. We need to be able to multiply this matrix and
the vector faster than just by performing a standard matrix-vector multiplication,