Java Reference
In-Depth Information
1
7
1
4
3
∞
5
∞
∞
0
3
11
2
2
12
∞
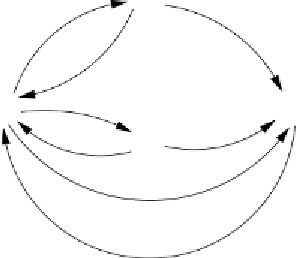
Figure16.1
An example of k-paths in Floyd's algorithm. Path 1, 3 is a 0-path
by definition. Path 3, 0, 2 is not a 0-path, but it is a 1-path (as well as a 2-path, a
3-path, and a 4-path) because the largest intermediate vertex is 0. Path 1, 3, 2 is
a 4-path, but not a 3-path because the intermediate vertex is 3. All paths in this
graph are 4-paths.
One solution is to run Dijkstra's algorithm for finding the single-source shortest
path (see Section 11.4.1) jVj times, each time computing the shortest path from a
different start vertex. If G is sparse (that is, jEj = (jVj)) then this is a good
solution, because the total cost will be (jVj
2
+ jVjjEjlogjVj) = (jVj
2
logjVj)
for the version of Dijkstra's algorithm based on priority queues. For a dense graph,
the priority queue version of Dijkstra's algorithm yields a cost of (jVj
3
logjVj),
but the version using
MinVertex
yields a cost of (jVj
3
).
Another solution that limits processing time to (jVj
3
) regardless of the num-
ber of edges is known as Floyd's algorithm. It is an example of dynamic program-
ming. The chief problem with solving this problem is organizing the search process
so that we do not repeatedly solve the same subproblems. We will do this organi-
zation through the use of the k-path. Define ak-path from vertex v to vertex u to
be any path whose intermediate vertices (aside from v and u) all have indices less
than k. A 0-path is defined to be a direct edge from v to u. Figure 16.1 illustrates
the concept of k-paths.
Define D
k
(v; u) to be the length of the shortest k-path from vertex v to vertex u.
Assume that we already know the shortest k-path from v to u. The shortest (k + 1)-
path either goes through vertex k or it does not. If it does go through k, then
the best path is the best k-path from v to k followed by the best k-path from k
to u. Otherwise, we should keep the best k-path seen before. Floyd's algorithm
simply checks all of the possibilities in a triple loop. Here is the implementation
for Floyd's algorithm.
At the end of the algorithm, array
D
stores the all-pairs
shortest distances.