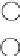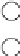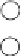Java Reference
In-Depth Information
A
A
OR
B
A
Figure15.6
Organizing comparisons for sorting five elements. First we order
two pairs of elements, and then compare the two winners to form a binomial tree
of four elements. The original loser to the root is labeled A, and the remaining
three elements form a sorted chain. We then insert element B into the sorted
chain. Finally, we put A into the resulting chain to yield a final sorted list.
• Recursively sort the winners.
• Fold in the losers.
We use binary insert to place the losers. However, we are free to choose the
best ordering for inserting, keeping in mind the fact that binary search has the
same cost for 2
i
through 2
i+1
1 items. For example, binary search requires three
comparisons in the worst case for lists of size 4, 5, 6, or 7. So we pick the order of
inserts to optimize the binary searches, which means picking an order that avoids
growing a sublist size such that it crosses the boundary on list size to require an
additional comparison. This sort is called merge insert sort, and also known as
the Ford and Johnson sort.
For ten elements, given the poset shown in Figure 15.7 we fold in the last
four elements (labeled 1 to 4) in the order Element 3, Element 4, Element 1, and
finally Element 2. Element 3 will be inserted into a list of size three, costing two
comparisons. Depending on where Element 3 then ends up in the list, Element 4
will now be inserted into a list of size 2 or 3, costing two comparisons in either
case. Depending on where Elements 3 and 4 are in the list, Element 1 will now be
inserted into a list of size 5, 6, or 7, all of which requires three comparisons to place
in sort order. Finally, Element 2 will be inserted into a list of size 5, 6, or 7.
Merge insert sort is pretty good, but is it optimal? Recall from Section 7.9 that
no sorting algorithm can be faster than (n log n). To be precise, the information
theoretic lower bound for sorting can be proved to be dlog n!e. That is, we can
prove a lower bound of exactly dlog n!e comparisons. Merge insert sort gives us
a number of comparisons equal to this information theoretic lower bound for all
values up to n = 12. At n = 12, merge insert sort requires 30 comparisons
while the information theoretic lower bound is only 29 comparisons. However, for
such a small number of elements, it is possible to do an exhaustive study of every
possible arrangement of comparisons. It turns out that there is in fact no possible
arrangement of comparisons that makes the lower bound less than 30 comparisons
when n = 12. Thus, the information theoretic lower bound is an underestimate in
this case, because 30 really is the best that can be done.