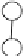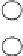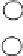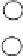Java Reference
In-Depth Information
Figure15.2
An example of building a binomial tree. Pairs of elements are
combined by choosing one of the parents to be the root of the entire tree. Given
two trees of size four, one of the roots is chosen to be the root for the combined
tree of eight nodes.
Looking at this another way, the only candidates for second place are losers to
the eventual winner, and our goal is to have as few of these as possible. So we need
to keep track of the set of elements that have lost in direct comparison to the (even-
tual) winner. We also observe that we learn the most from a comparison when both
competitors are known to be larger than the same number of other values. So we
would like to arrange our comparisons to be against “equally strong” competitors.
We can do all of this with a binomial tree. A binomial tree of height m has 2
m
nodes. Either it is a single node (if m = 0), or else it is two height m1 binomial
trees with one tree's root becoming a child of the other. Figure 15.2 illustrates how
a binomial tree with eight nodes would be constructed.
The resulting algorithm is simple in principle: Build the binomial tree for all n
elements, and then compare the dlog ne children of the root to find second place.
We could store the binomial tree as an explicit tree structure, and easily build it in
time linear on the number of comparisons as each comparison requires one link be
added. Because the shape of a binomial tree is heavily constrained, we can also
store the binomial tree implicitly in an array, much as we do for a heap. Assume
that two trees, each with 2
k
nodes, are in the array. The first tree is in positions 1
to 2
k
. The second tree is in positions 2
k
+ 1 to 2
k+1
. The root of each subtree is in
the final array position for that subtree.
To join two trees, we simply compare the roots of the subtrees. If necessary,
swap the subtrees so that tree with the the larger root element becomes the second
subtree. This trades space (we only need space for the data values, no node point-
ers) for time (in the worst case, all of the data swapping might cost O(n log n),
though this does not affect the number of comparisons required). Note that for
some applications, this is an important observation that the array's data swapping
requires no comparisons. If a comparison is simply a check between two integers,
then of course moving half the values within the array is too expensive. But if a
comparison requires that a competition be held between two sports teams, then the
cost of a little bit (or even a lot) of book keeping becomes irrelevent.
Because the binomial tree's root has log n children, and building the tree re-
quires n1 comparisons, the number of comparisons required by this algorithm is
n + dlog ne 2. This is clearly better than our previous algorithm. Is it optimal?