Information Technology Reference
In-Depth Information
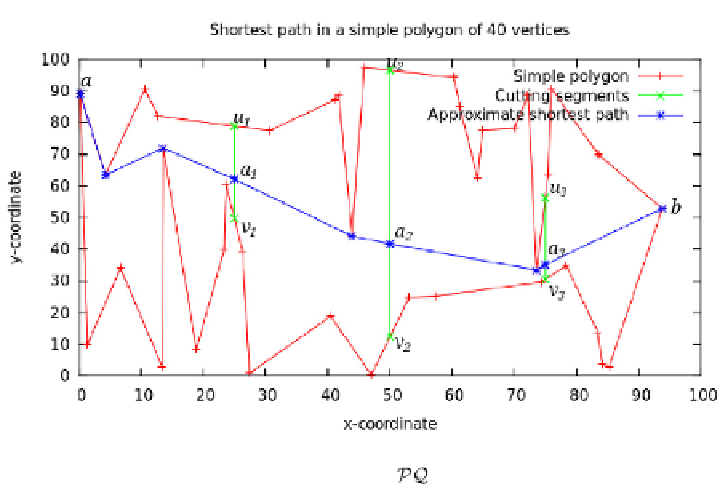
Fig. 4.
The shortest path between
a
and
b
in is obtained by Algorithm 1, where
[
u
i
,v
i
] is cutting segments, for
i
=1
,
2
,
3.
SP
(
p, q
)=
∪
i
=0
SP
(
a
i
,a
i
+1
), where
a
0
=
a
,
a
4
=
b
,and
a
i
∈
[
u
i
,v
i
]for
i
=1
,
2
,
3
3 Performance Analysis
3.1 Run Time
We now consider the run time of Algorithm 1. Due to the funnel algorithm a
triangulation of polygon is first required. We used the implementation of the
triangulation algorithm given in [
9
]. That is an improved version of the ear
removal algorithm. The complexity is
O
(
n
2
), where
n
is the number of vertices
of the polygon. If we triangulate whole
D
then it will take a long time. By
dividing
T
i
the size of polygons needed to triangulate, is
then smaller. The time of triangulating sub-polygons is consequently reduced.
Therefore, the total time of triangulating
D
into sub-polygons
T
i
,for
i
=0
,...,k
, is theoretically
small as a larger number of cutting segments.
The algorithm runs on the polygon
are monotone with
respect to
x
-coordinate without three collinear points. The number of vertices
of the polygon is 350000. We run the algorithm for several sets of cutting seg-
ments. In Table
1
, the run time of Algorithm 1 is reduced significantly as the
cutting segments is increased. This was stated clearly in [
1
]aswell.Here,we
measure in more detail the time required for triangulating and dual tree con-
structing invoked in the funnel algorithm. Table
1
also shows that if the number
of cutting segments is small then the run time of the triangulation and dual trees
construction take almost the run time of the Algorithm 1. This indicates that if
we choose an appropriate number of cutting segments, the method is ecient,
specially in case of huge data.
PQ
in which
P
and
Q
Search WWH ::

Custom Search