Image Processing Reference
In-Depth Information
whole piece is not thrown out, just the piece's individual metric(s). FPC updates each Classi-
ier object with the new mean(s) and standard deviation(s) and then produces TXT files with
the same information.
Figure 11
provides an example to illustrate the process.
FIGURE 11
Flow chart for collecting Classifier statistics.
Example: Pieces 1-10 belong to Classifier A, Pieces 11-20 to Classifier B, and Pieces 21-30
to Classifier C. The mean for metric X from Pieces 1-10 is calculated to be 15 (as in 15%)
and the standard deviation is 5 (as in 5% points). If Piece 10's metric X is 31, which is greater
than 15 + 3 × 5 (
z
-test upper-bound), it is an outlier. Piece 10's metric X is therefore discarded
and the mean and standard deviation for metric X are recomputed using Pieces 1-9. Classifi-
er A then receives the new mean and standard deviation for metric X, and a TXT file is writ-
ten. These steps are repeated for Classifiers B and C.
6 Classifying Test Pieces
Three techniques were used to classify test pieces from metric data: Unweighted Points,
Weighted Points, and Euclidean Distance.
6.1 Classification Techniques
Unweighted Points is the simplest technique. It treats each metric equally, assigning a single
point to a Classifier each time one of its metrics best matches the test piece. The classifier with
the most points at the end is declared the winner and is chosen as the classification for the test
piece.
Weighted Points was an original approach. It works similar to Unweighted Points except
metrics can be worth different amounts of points. First, it calculates metric differences from
the Classifiers: For each metric, it finds the Classifier with the highest value and the one with
the lowest value. It subtracts the lowest value from the highest value, and the difference be-
comes the number of “points” that metric is worth. Then, like Unweighted Points, it looks to
see which Classifier is closest to the test piece for each particular metric, only instead of as-
signing a single point, it assigns however many points the metric is worth.
Euclidean Distance is a standard technique for calculating distances in high-dimensional
space. Here, it focuses on one Classifier at a time, taking the square root of the sums of each
metric difference (between test piece and classifier) squared. This is illustrated in
Figure 12
,
where
p
is the classifier,
q
is the test piece, and there are
n
metrics.
FIGURE 12
Euclidean distance formula.
Euclidean distance is calculated for each classifier, and the classifier with the smallest dis-
tance from the test piece is chosen as the classification.

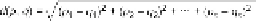
Search WWH ::

Custom Search