Image Processing Reference
In-Depth Information
The CDF-based kernel showed much greater performance in this example. The kernel val-
ues
k
12
and
k
13
clearly reflect the larger deviation (less similarity) of the third distribution from
the original.
This is due to the fact that the density-based Bhatacharyya kernel does not capture the glob-
al variations. The CDF-based kernel is much more effective in detecting global changes in the
distributions.
5 Generalization
This method can be extended to high-dimensional distributions. Let
F
and
G
be
n
-dimensional
CDFs for the random variables with bounded ranges. Then we can define the distance meas-
ures similar to the 1D case.
When
p
= 2, a kernel can also be defined from the distance
d
2
(
F
,
G
).
The advantages of CDF can be maintained in the high-dimensional cases. For example, the
translation invariance and the scaling property can be established in a similar fashion. The
2D extension is especially interesting because it is directly associated with image process-
ing. However, there exist challenges commonly associated with extensions to high-dimension-
al spaces. For example, there will be significant cost in directly computing high-dimension-
al CDFs. If
m
points are used to represent a 1D CDF, an
n
-dimensional CDF would need
m
n
points.
6 Conclusions and Future Work
In this paper, we presented a new family of distance and kernel functions on probability dis-
tributions based on the cumulative distribution functions. The distance function was shown
to be a metric and the kernel function was shown be a positive definite kernel. Compared to
the traditional density-based divergence functions, our proposed distance measures are more
efective in detecting global discrepancy in distributions. Invariance properties of the distance
functions related to translation, reflection, and scaling are derived. Experimental results on
generated distributions were discussed.

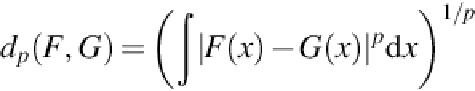
Search WWH ::

Custom Search