Image Processing Reference
In-Depth Information
where Γ(
μ
,
ν
) denotes the set of all couplings of
μ
and
ν
. EMD does measure the global move-
ments between the distributions. However, the computation of EMD involves solving optim-
ization problems and is much more complex than the density-based divergence measures.
Related to the distance measures are the statistical tests to determine whether two samples
are drawn from different distributions. Examples of such tests include the Kolmogorov-
3 Distances on cumulative distribution functions
A cumulative distribution function (CDF) of a random variable
X
is defined as
Let
F
and
G
be CDFs for the random variables with bounded ranges (i.e., their density func-
tions have bounded supports). For
p
≥ 1, we define the distance between the CDFs as
It is easy to verify that
d
p
(
F
,
G
) is a metric. It is symmetric and satisfies the triangle inequal-
ity. Because CDFs are left-continuous,
d
p
(
F
,
G
) = 0 implies that
F
=
G
.
When
p
= 2, a kernel can be derived from the distance
d
2
(
F
,
G
):
To show that
k
is indeed a kernel, consider a kernel matrix
M
= [
k
(
F
i
,
F
j
)], 1 ≤
i
,
j
≤
n
. Let [
a
,
b
]
be a finite interval that covers the support of all density functions
p
i
(
x
), 1 ≤
i
≤
n
.
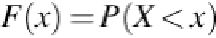
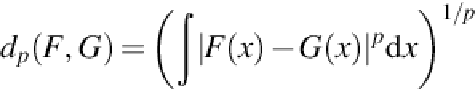
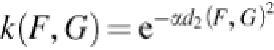
Search WWH ::

Custom Search