Image Processing Reference
In-Depth Information
All these similarity/dissimilarity measures are based on the point-wise comparisons of the
probability density functions. As a result, they are inherently local comparison measures of
the density functions. They perform well on smooth, Gaussian-like distributions. However, on
discrete and multimodal distributions, they may not reflect the similarities and can be sensit-
ive to noises and small perturbations in data.
Example 1
Let
p
be the simple discrete distribution with a single point mass at the origin and
q
the
perturbed version with the mass shifted by
a
(
Figure 1
).
FIGURE 1
Two distributions.
The Bhatacharyya ainity and divergence values are easy to calculate:


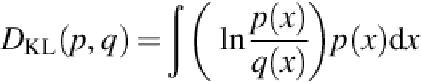

Search WWH ::

Custom Search