Image Processing Reference
In-Depth Information
In this paper, we propose a family of distances and kernels that are defined on the cumu-
lative distribution functions, instead of densities. This work is an extension of our previous
This paper is organized as follows.
Section 2
introduces traditional kernels and distances
tions based on cumulative distribution functions is proposed. Experimental results on Gaussi-
of the method to higher dimensional spaces.
Section 6
provides conclusions and proposals for
improvements.
2 Distance and Similarity Measures Between
Distributions
Given two probability distributions, there are well-known measures for the differences or sim-
ilarities between the two distributions.
In [
4
], the probability product kernel is deined as a generalization of Bhatacharyya ainity:
The Bhatacharyya distance is a dissimilarity measure related to the Bhatacharyya ainity:
The Hellinger distance ([
5
]) is another metric on distributions:

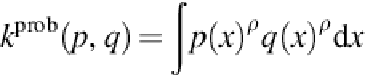
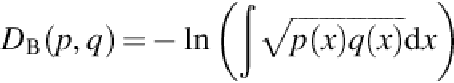
Search WWH ::

Custom Search