Image Processing Reference
In-Depth Information
(3)
The above equations are rearranged using radius
R
as
(4)
3.3 Distortion Coefficient Estimation of the FOV Model
line after being projected onto a 2D surface by a camera if there is no distortion. This means
that the larger the difference between an actual straight-line component and a projected
straight line, the larger the distortion is. Conversely, the less the difference is, the less the dis-
tortion is. The degree of camera distortion can be verified by the distortion coefficient
ω
of the
FOV model. In the FOV model,
q
ωi
is a point of restoration of distorted point
p
i
by the distor-
tion coeicient
ω
. The distortion parameter estimation from Ref. [
9
] expresses a relationship
of
D
- 1
(
ω, p
i
) with regard to the distortion coefficient, which can solve the linear equation of the
least squares distance when the estimation is applied to the algorithms from
p
1
to
p
n
.
By solving the equation of the
i
and
j
functions where the error function
E
ij
(
ω
) is minimized
with regard to the distortion coefficient
ω
, the distortion coefficient
ω
can be estimated. Using
this method, distortion correction can be performed by using the distortion correction coei-
cient with regard to the camera distortion center.
(5)
(6)

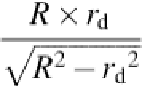

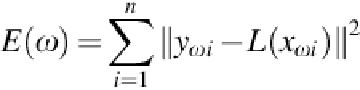
Search WWH ::

Custom Search