Image Processing Reference
In-Depth Information
(20)
In Ref. [
20
], the author introduced two sets of invariant descriptors
I
and
J
which are, re-
(21)
(22)
and stable. The completeness guarantees the uniqueness of matching. The stability gives ro-
demonstrates that the shape space
S
can be considered as a metric space with a set of metrics.
used to compare the evolving curve and the available templates.
(23)
For any real number
p
such that
p
> 1. Where
f
and
h
are two normalized affine arc
length reparametrization of two objects having, respectively, the shapes
F
and
H
. The shape
having the minimum distance according to the evolving active contour is used as template.
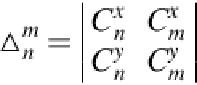
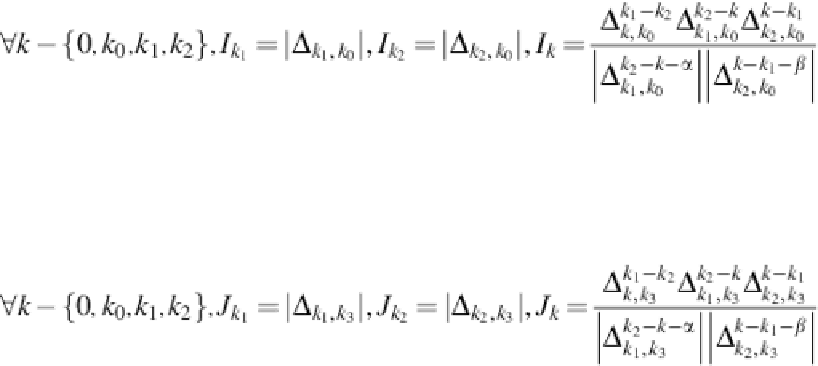
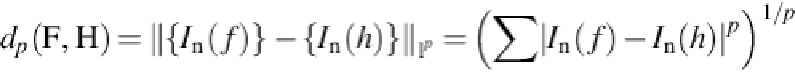
Search WWH ::

Custom Search