Image Processing Reference
In-Depth Information
Table 2
The Estimated Affine Motion Parameters
l
0
α
A
Shapes of (b) 0.002 1.003
Shapes of (d) 0
2.004
2.3 Discussion
Having the parameters of the affine or Euclidean transformations between the two contours,
we perform the alignment of the two curves to determine the regions of variability between
shapes by computing the product function of the signed distance functions associated to level
set functions of, respectively, the target and the reference object after alignment given by
(19)
where and
f
∅
are the two binary images associated, respectively, to ∅
ref
and ∅. See Ref.
variability between the two binary images and
f
∅
due to occlusion, cluter, or missing
parts, whereas in positive regions, the objects are similar. Thus, in what follows, we propose
to update the level set function ∅, only in regions of variability between shapes to make the
evolving contours overpass the spurious edges and recover the desired shapes of objects. This
property recalls the narrow band technique used to accelerate the evolution of the level set
2.4 Global Matching Using Affine Invariants Descriptors
In presence of many templates, we have to choose the most suitable one according to the
evolving curve. Let
α
and
β
be positive real numbers, and
k
0
, k
1
, k
2
, and
k
3
four positive integers.
Let
C
n
x
and
C
n
y
be the complex Fourier coefficients of the coordinates (
u
,
v
). Δ denotes the
determinant.











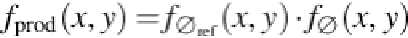
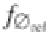


Search WWH ::

Custom Search