Image Processing Reference
In-Depth Information
Table 1
The Estimated Parameters of Synthetic Rigid Motion
Rotation (°) Scaling Difference Between Starting Point
−45
1
0
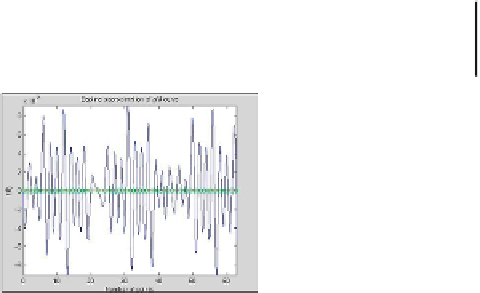
FIGURE 2
Example
g
(
l
)'s curve.
2.2 Affine Shape Alignment
In order to define affine invariant shape prior from a reference shape, we have to perform
shape matching between the target and the template shapes
F
1
and
F
2
. To correctly estimate
the affine motion parameters, we have to deal with the same number of points which is not
proposes to use the affine reparametrization of curve which is invariant under affine trans-
formation. We will start by presenting the affine reparametrization procedure of a given curve.
Then we will describe our method of affine motion's parameters estimation.
2.2.1 Reparametrization of closed curve
If we take the same object in two different camera sides, we found a different number of con-
tour points in each image. Consequently, we proceed by normalization of curves under af-
ine transformation. Given the shape front, its edge pixels are extracted and traversed to yield
a discrete closed curve which is a parametric equation
γ
(
t
) = (
u
(
t
),
v
(
t
)), where
t
∈ {0,…,
N
− 1}
and
γ
(
N
) =
γ
(0). We use the affine arc length reparametrization to normalize closed curves un-
der affine transformations that can be expressed by:
(8)





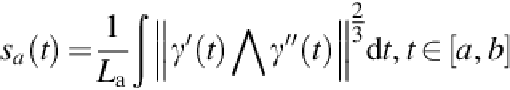

Search WWH ::

Custom Search