Image Processing Reference
In-Depth Information
(1)
Let
γ
1
and
γ
2
be centered (according to the center of mass) and normalized arc length para-
meterizations of two closed planar curves having shapes
F
1
and
F
2
. Suppose that
γ
1
and
γ
2
have
a similar shape under rigid transformation.
In shape space this is equivalent to have:
(2)
where
α
is the scaling factor,
θ
the rotation angle,
t
0
is the difference between the two starting
points of
γ
1
and
γ
2
.
Rigid motion estimation is obtained by minimizing the following quantity introduced by
(3)
the Hausdorff distance between the two shapes. In practice, this result implies the uniqueness
of the motion's parameters so obtained. Using Fourier descriptors
C
k
(
γ
1
) and
C
k
(
γ
2
), minimiz-
ing
E
rr
becomes equivalent to minimize
f
(
θ
,
t
0
) in Fourier domain
(4)
[
18
]
proposed an analytical solution to compute
t
0
and
θ
.
t
0
is one of the zeros of the following
function:
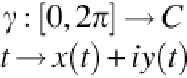
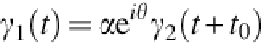


Search WWH ::

Custom Search