Image Processing Reference
In-Depth Information
(14)
Let's assume that |
F
| =
n
,
m
is the number of angle intervals and
l
is the length of the video
segment in terms of seconds. With these assumptions, the representation of a video segment
using average of optical flow vectors with angular grouping can be formulized as
(15)
Above vector representation is composed of
m
dimensions each of which is the magnitude
of the sum of optical flow vectors for angle intervals. This is the common way of optical flow
representation except the usage of vectors instead of histograms. This representation is de-
scriptive as it utilizes the movement of a segment in different angel intervals by using the vec-
tor sum and magnitude calculation. But, it lacks the temporal information in terms of velocity.
This means that the flow details throughout the frame sequence are discarded by only look-
ing at the resulting direction and magnitude information. If this vector is extracted for each
problem arises. The dimension of the resulting vector will be
m
x
n
x
l
. For a 30-fps video of 5 is
length with 30 angular intervals, for example, a vector of 4500 features is obtained for repres-
enting a segment. Using a frequency filter of 0.2 (6 frames selected from a second of the video)
will decrease the dimension into 900, but the problem will not be able to be solved yet. This
with the newly proposed time-series classification method including the new distance metric
for the feature vectors.
In our approach, we enrich the representation to make the temporal information more de-
scriptive without causing the curse of dimensionality problem. For this purpose, a new com-
ponent is needed for the above feature representation based on movement magnitude of the
segment in different directions. Velocity is selected as the fundamental idea for the new com-
ponent as the velocity of the frames strongly affects the nature of video motion such as in walk
and run events. For this purpose, weighted frame velocity concept is proposed. Abstractly, the
velocity component is added to the feature vector to contain distance-velocity pair.
Weighted frame velocity is a metric which measures the velocity of a segment in a given di-
mension. It is weighted with the vector count in its direction. Theoretically, weighted frame
velocity is formulated inspiring from the general velocity calculation
:
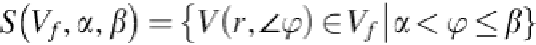
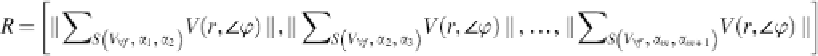
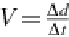
Search WWH ::

Custom Search