Image Processing Reference
In-Depth Information
These definitions are easily extended to fuzzy sets for dealing with uncertainty. The dein-
ition of rough fuzzy sets we propose to adopt here takes inspiration, as firstly made in Ref.
on
T
defined by adding to each element of
T
the degree of its membership to the set through a
mapping
μ
F
:
T
→ [0, 1]. The operations on fuzzy sets are extensions of those used for conven-
tional sets (intersection, union, comparison, etc.). The basic operations are the intersection and
union as defined as follows:
The previous are only a restricted set of operations applicable among fuzzy sets, but they
are the most significant for our aim. A
composite set
or
C
-set is a triple
C
= (
Γ
,
m
,
M
) (where
Γ
= {
T
1
, …,
T
p
} is a partition of
T
in
p
disjoint subsets
T
1
, …,
T
p
, while
m
and
M
are mappings of
kind
T
→ [0, 1] such that
and
where
(1)
for each choice of function
f
:
T
→[0, 1].
Γ
and
f
uniquely define a composite set. Based on these
assumptions, we may formulate the following definition of rough fuzzy set:
1. If
f
is the membership function
μ
F
and the partition
Γ
is made with respect to a relation
, i.e.,
Γ
=
T
/ , a fuzzy set
F
gets two approximations
RS
−
(
F
) and
RS
−
(
F
), which are
again fuzzy sets with membership functions defined as Equation
(1)
, i.e.,
and
. The couple of sets (
RS
−
(
F
),
RS
−
(
F
)) is a
rough fuzzy set
.









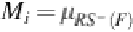
Search WWH ::

Custom Search