Image Processing Reference
In-Depth Information
(5)
Let
V
(
u
,
v
),
U
(
u
,
v
), and
F
(
u
,
v
) present the probability densities of
v
(
i
,
j
),
u
(
i
,
j
), and
f
(
i
,
j
), re-
spectively. Equation
(5)
can be expressed as
(6)
Making the approximation that ln
u
and ln
f
are uncorrelated random variables, Equation
(6)
is found by convolution as follows:
(7)
The multiplication corrupts the field and a division can undo the corruption. In the fre-
quency domain, multiplications and divisions convert to convolutions and deconvolutions as
follows:
(8)
In which
V
,
U
, and
F
are probability densities. After this stage, the uniformity distribution
(
F
) is modeled and viewed as blurring intensity distribution
U
that is the main stage for cor-
recting bias field.
2.4.2 Correction step
An straightforward technique for image bias field correction would be that if the spatial fre-
quencies of
u
(
i
,
j
) (the true image) and
f
(
i
,
j
) bias field are disjointed, the bias field can be re-
moved by filtering out the spatial frequencies illustrating the bias field. In some cases, use-
ful knowledge in MRI related to higher spatial frequencies than the intensity nonuniform-
ity. Thus, by removing low spatial frequencies, intensity nonuniformity can be suppressed.
The problem is that in most cases, spatial frequency information of the bias field and true im-
age are not perfectly separated, and they have some overlapped components. For example,
in MRI scans, when low spatial frequencies are removed, the spatial image will be consider-
ably changed, implying the existence of useful knowledge at low spatial frequency bands. In
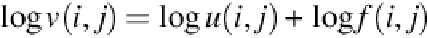
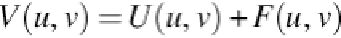


Search WWH ::

Custom Search